Question

Prove by vector method that the triangle inscribed in a semicircle is a right angle triangle.

Answer 1

We prove the statement by triangle law of vector addition and use the concept of direction in vectors to show that vectors in opposite direction but equal magnitude have opposite signs. Then we find the vector product of two sides which results in a zero giving sin of the angle zero.

• Triangle law of vector addition states that if two sides of a triangle are represented by vectors then the third side of the triangle can be written as the resultant vector which is addition of two vectors.
• Cross product of two vectors $\overrightarrow a \times \overrightarrow b = ab\sin \theta$

Complete step-by-step answer:
First we draw a semi-circle and draw a triangle inside it which is represented by vectors as its sides.

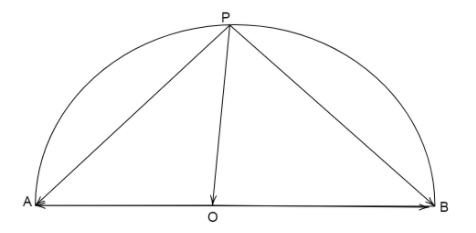
Here O is the center of the circle and the point P lies on the circle and $AO = OB$ is the radius of the circle.
When we drop vectors from point P to points A, B, O and the vectors from center O to the points A, B.
Then vectors $\overrightarrow {PO} ,\overrightarrow {PA} ,\overrightarrow {PB}$ and $\overrightarrow {OA} ,\overrightarrow {OB}$ are formed.
Considering the triangle $PAO$
By triangle law of vector addition we can write
$\overrightarrow {PA} = \overrightarrow {PO} + \overrightarrow {OA}$ … (1)
Considering the triangle $PBO$
By triangle law of vector addition we can write
$\overrightarrow {PB} = \overrightarrow {PO} + \overrightarrow {OB}$ … (2)
Since, the vectors $\overrightarrow {OA} ,\overrightarrow {OB}$ both have directions in opposite sides but are equal to the radius of the circle in magnitude, so we can write $\overrightarrow {OA} = - \overrightarrow {OB}$
Substitute the value of $\overrightarrow {OA} = - \overrightarrow {OB}$ in equation (1)
$\overrightarrow {PA} = \overrightarrow {PO} - \overrightarrow {OB}$
Now we take cross product of two vectors $\overrightarrow {PA} ,\overrightarrow {PB}$
$\overrightarrow {PA} \times \overrightarrow {PB} = (\overrightarrow {PO} - \overrightarrow {OB} ) \times (\overrightarrow {PO} + \overrightarrow {OB} )$
Since, we know $(\overrightarrow a + \overrightarrow b ) \times (\overrightarrow a - \overrightarrow b ) = \left| {(a - b)(a + b)} \right|\sin \theta = \left| {{a^2} - {b^2}} \right|$
{since $(a - b)(a + b) = {a^2} - {b^2}$}
Therefore, substitute $\overrightarrow a = \overrightarrow {PO} ,\overrightarrow b = \overrightarrow {PB}$ and the angle $\angle APB$ which lies between the two vectors.

$$\overrightarrow {PA} \times \overrightarrow {PB} = \left| {(PO - OB)(PO + OB)} \right| \\\ \overrightarrow {PA} \times \overrightarrow {PB} = \left| {P{O^2} - O{B^2}} \right| \\\ \overrightarrow {PA} \times \overrightarrow {PB} = \left| {P{O^2}} \right| - \left| {O{B^2}} \right| \\\$$

Since, $\overrightarrow {PO} ,\overrightarrow {PB}$ are both radius vectors, therefore they are equal in magnitude and from the diagram we see they are equal in direction as well.
So, $\overrightarrow {PO} = \overrightarrow {PB}$
$\Rightarrow \overrightarrow {PA} \times \overrightarrow {PB} = \left| {P{O^2}} \right| - \left| {P{O^2}} \right| = 0$
Therefore, $\Rightarrow \overrightarrow {PA} \times \overrightarrow {PB} = 0$
We know vector multiplication opens as
$\Rightarrow PA.PB \sin (APB) = 0$
Since sides of triangle cannot be zero, so

$$\Rightarrow \sin (APB) = 0 \\\ \sin (APB) = \sin {90^ \circ } \\\ \angle APB = {90^ \circ } \\\$$

Therefore, a triangle inscribed in a semicircle is a right angle triangle.

Note: Students can make mistakes while taking the directions of vectors, always keep in mind the direction is from the starting point to the end point in which direction the array points. Also, in triangle law of vector addition we add the vectors which move along the same direction.