Question

Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.

Answer 1

Hint : In order to solve this question first we have to assume that the all three internal bisectors of the angles of the triangle are intersecting each other. Now if we can prove that this intersection point is common in all of the internal bisectors then we can say that the internal bisectors are concurrent. According to the definition of concurrent lines the lines should intersect each other at a single common point.

Complete step-by-step answer :
Given:

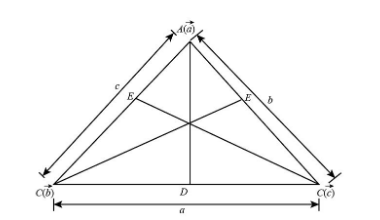
Let us assume in a triangle $\Delta ABC$ have the side lengths $AB = c$ , $BC = a$ and $CA = b$ respectively. The position vectors of the vertices of the triangle A, B and C are $\vec a$ , $\vec b$ and $\vec c$ respectively.
Now drawing the internal bisectors of the three internal angles of the triangle $\angle A,{\rm{ }}\angle B{\rm{ and }}\angle {\rm{C}}$ we have.
$\Rightarrow$ The internal bisector of the angle $\angle A$ is $AD$ .
$\Rightarrow$ The internal bisector of the angle $\angle B$ is $BE$ .
$\Rightarrow$ The internal bisector of the angle $\angle C$ is $CF$ .
Also,
Now according to the theorem, we know that “the Internal bisectors of the triangle divide the opposite sides in the ratio of the sides containing the angles”.
In the internal bisector AD, the point D divides the sides AB and AC in the ratio of $AB:AC = c:b$
So, the position vector of D is given by,

$$\Rightarrow \vec D = \dfrac{{\left( {AB \times \vec c + AC \times \vec b} \right)}}{{AB + AC}}\\\ = \dfrac{{\left( {c\vec c + b\vec b} \right)}}{{c + b}}$$

Similarly, in the bisector BE, the point E divides the sides AB and BC in the ratio of $AB:BC = c:a$
So, the position vector of E is given by,
$\Rightarrow \vec E = \dfrac{{\left( {AB \times \vec c + BC \times \vec a} \right)}}{{AB + BC}}\\\ = \dfrac{{\left( {c\vec c + a\vec a} \right)}}{{c + a}}$
And, in the bisector CF, the point F divides the sides BC and AC in the ratio of $BC:AC = a:b$
So, the position vector of F is given by –
$\Rightarrow \vec F = \dfrac{{\left( {BC \times \vec a + AC \times \vec b} \right)}}{{BC + AC}}\\\ = \dfrac{{\left( {a\vec a + b\vec b} \right)}}{{a + b}}$
Now we have to find the point that divides the internal bisectors AD, BE and CF and if the point that divides these bisectors is the same for each of the bisectors then we can say that the internal bisectors of the angles of a triangle are concurrent.
Let us assume that the points dividing the internal bisectors AD, BE and CF are L, M and N respectively.
So now,
The position vector point L dividing the internal bisector AD in two parts in the ratio of $\left( {AC + AB} \right):AB = \left( {b + c} \right):a$ is
$\Rightarrow \vec L = \dfrac{{AC \times \vec b + AB \times \vec c + BC \times \vec a}}{{AC + AB + BC}}\\\ = \dfrac{{b\vec b + c\vec c + a\vec a}}{{b + c + a}}$
Similarly, the position vector of point M dividing the internal bisector BE in two parts in the ratio of $\left( {BC + AB} \right):AC = \left( {a + c} \right):b$ is
$\Rightarrow \vec M = \dfrac{{BC \times \vec a + AB \times \vec c + AC \times \vec b}}{{BC + AB + AC}}\\\ = \dfrac{{a\vec a + c\vec c + b\vec b}}{{a + c + b}}$ -

And the position vector of point N dividing the internal bisector CF in two parts in the ratio of $\left( {BC + AC} \right):AB = \left( {a + b} \right):c$ is
$\vec N = \dfrac{{BC \times \vec a + AC \times \vec b + AB \times \vec c}}{{BC + AC + AB}}\\\ = \dfrac{{a\vec a + b\vec b + c\vec c}}{{a + b + c}}$
Now we see that the values of the position vectors of the points L, M and N dividing the internal bisectors AD, BE and CF respectively are the same. So, we can say that this point lies in all of the internal bisectors and it means that all of the bisectors cross each other at this point.
Therefore, we can say that the internal bisectors of the angles of a triangle are concurrent.

Note : The alternate method of solving this question was using the Coordinate Method. In this method we obtain the linear equations of the lines AD, BE and CF using the coordinates of the points and then finding the determinant value of these equations and if the value of the determinant is equal to zero then, the lines are said to be concurrent.