Question

Prove by vector method that $\cos (A + B) = \cos A\cos B - \sin A\sin B$.

Answer 1

Here in this question we should know the vector components, vector dot product and basic trigonometric terminologies.
Vector components: - If we have a vector A then its components along x and y direction is as follow $\mathop A\limits^ \to = {A_x}\mathop i\limits^ \wedge + {A_y}\mathop j\limits^ \wedge$
$\mathop A\limits^ \to = \cos \theta \mathop i\limits^ \wedge + \sin \theta \mathop j\limits^ \wedge$
Dot product: - It is a scalar product of the two vectors. The formula is given by $\widehat A.\widehat B = \left| {\mathop A\limits^ \to } \right|\left| {\mathop B\limits^ \to } \right|\cos \theta$ where ‘A’ and ‘B’ are the two vectors

Complete step-by-step answer:
With the help of graphs we will solve this question so that clarity is more.

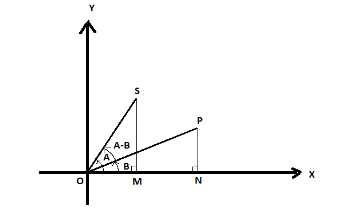
Construction: - Draw the two vectors OS and OP making $\angle A$ and $\angle B$ with the x-axis also draw line SM and PN such that they are perpendicular to the x-axis. And $\angle (A - B)$ is the angle between the two vectors.
Now from the figure we can see that $\widehat {OS} = \overrightarrow {OM} + \overrightarrow {SM}$ and $\widehat {OP} = \overrightarrow {ON} + \overrightarrow {PM}$
Using vector components we can write these equations as: -
$\widehat {OS} = \widehat i\cos A + \widehat j\sin A$ ...............equation 1.
$\widehat {OP} = \widehat i\cos B + \widehat j\sin B$ ................equation 2.
Now by definition of vectors dot product we can apply this formula $\widehat A.\widehat B = \left| {\mathop A\limits^ \to } \right|\left| {\mathop B\limits^ \to } \right|\cos \theta$
$\widehat {OS}.\widehat {OP} = \left| {\overrightarrow {OS} } \right|\left| {\overrightarrow {OP} } \right|\cos (A - B)$
$\widehat {OS}.\widehat {OP} = 1 \times 1 \times \cos (A - B)$ (Magnitude of unit vectors is 1)
$\widehat {OS}.\widehat {OP} = \cos (A - B)$ ...............equation 3.
Putting value of equation 1 and 2 in 3 we will get
$(\widehat i\cos A + \widehat j\sin A).(\widehat i\cos B + \widehat j\sin B) = \cos (A - B)$ (Dot product of$(\widehat i).(\widehat i) = 1$and $(\widehat j).(\widehat j) = 1$)
$(\cos A\cos B + \sin A\sin B) = \cos (A - B)$
Hence it’s proved that $(\cos A\cos B + \sin A\sin B) = \cos (A - B)$ with the help of a vector method.

Note: For solving such types of questions students must be cautious while doing dot products.
Dot product formula is $\widehat A.\widehat B = \left| {\mathop A\limits^ \to } \right|\left| {\mathop B\limits^ \to } \right|\cos \theta$ where $\left| {\mathop A\limits^ \to } \right|$ and $\left| {\mathop B\limits^ \to } \right|$ are the unit vectors whose magnitude is 1 as the name suggests unit means one.
Dot products of the same components:-
$(\widehat i).(\widehat i) = 1$ ($(\widehat i)$Represents direction in x-axis)
$(\widehat j).(\widehat j) = 1$ ($(\widehat j)$Represents direction in y-axis)
$(\widehat k).(\widehat k) = 1$ ($(\widehat k)$Represents direction in z-axis)