Question
Question: Prove by using vector \[\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alp...
Prove by using vector
cos(α−β)=cosαcosβ+sinαsinβ
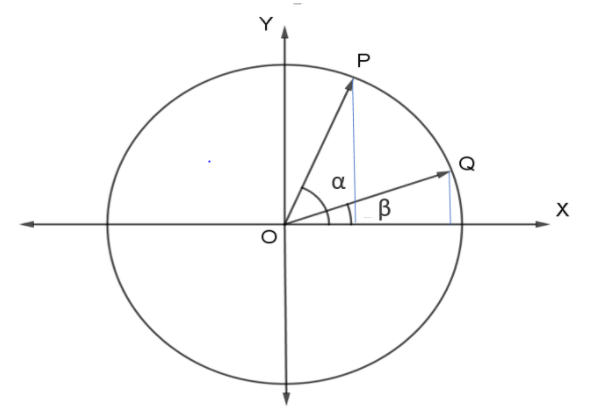
Solution
It is sometimes useful to write a vector v in terms of its magnitude and argument rather than rectangular form ai+bj. This is done using the sine and cosine functions. The r(cosαi+sinαj) version of v is called trigonometric form. Since cosαi+sinαj=1 the trigonometric form expresses v as a scalar multiple of a unit vector in the same direction as v.
Complete step by step solution:
Consider a unit circle.
Draw two-unit vectors OPand OQ with an angle of
Now as we have described in hint:0
OP=cosαi+sinαj……(1) OQ=cosβi+sinβj……(2)The scalar product OPand OQof two vectors OP and OQ is a number defined by the equation
OP⋅OQ=OPOQcos(α−β)=cos(α−β)……(3)
where αand β is the angle between the vectors.
Also from equation (1) and (2)
So with the equation (3) and (4)
⇒cos(α−β)=cosα⋅sinβ+sinα⋅cosβ
Hence Proved.
Note:
Sometimes people forget when to use sin or cos for calculating vector components. It is important to note that the dot product always results in a scalar value. Furthermore, the dot symbol “.” always refers to a dot product of two vectors, not traditional multiplication of two scalars as we have previously known.
