Question

Protons and singly ionized atoms of ${{U}^{235}}$ and ${{U}^{238}}$ are passed in turn (which means one after the other and not at the same time) through a velocity selector and then enter a uniform magnetic field. The protons describe semicircles of radius 10mm. The separation between the ions of ${{U}^{235}}$ and ${{U}^{238}}$ after describing semicircle is given by

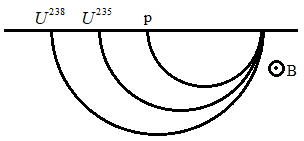
A. 60 mm
B. 30 mm
C. 2350 mm
D. 2380 mm

Answer 1

We are given protons and singly ionized atoms of ${{U}^{235}}$ and ${{U}^{238}}$ which is passed in turn through a velocity selector and then made to enter a uniform magnetic field. We are given the radius of the semicircle of the proton and asked to find the distance of separation of the other two. Using the given radius of proton we can find the magnetic field and thus the radius of the other two. Using the radius, from the figure we can calculate their distance of separation.

Formula used:
$F=\dfrac{m{{v}^{2}}}{r}$
$F=Bqv$

Complete step by step answer:
In the question we are given a proton and singly ionized atoms of ${{U}^{235}}$ and ${{U}^{238}}$. It is said that they are passed in turn through a velocity selector and then made to enter a magnetic field.
We are also given the radius of the proton as 10 mm.
We know that when the proton is revolving in a circular path it will have a centripetal force given by,
$F=\dfrac{m{{v}^{2}}}{r}$, where ‘m’ is the mass, ‘v’ is the velocity and ‘r’ is the radius.
Therefore for the proton we know that,
$m=1unit$
$r={{r}_{p}}=10mm$
$\Rightarrow F=\dfrac{1\times {{v}^{2}}}{{{r}_{p}}}$
$\Rightarrow F=\dfrac{1\times {{v}^{2}}}{10}$
We also know that there will be a force due to the magnetic field which is given as,
$F=Bqv$, where ‘B’ is the magnetic field, ‘q’ is the charge and ‘v’ is the velocity.
For the proton we know that,
$q=1e$
Therefore we can write,
$\Rightarrow F=Bv$
By equating these two forces we will get,
$\Rightarrow \dfrac{{{v}^{2}}}{10}=Bv$
$\therefore B=\dfrac{v}{10}$
Thus we get the magnetic field as, $B=\dfrac{v}{10}$
Now let us consider the figure given below.

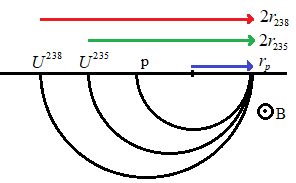
Here ‘${{r}_{235}}$’ is the radius of ${{U}^{235}}$and ‘${{r}_{238}}$’ is the radius of ${{U}^{238}}$.
From the figure we can see that the separation between ${{U}^{235}}$ and ${{U}^{238}}$is,
$S=2{{r}_{238}}-2{{r}_{235}}$
$\Rightarrow S=2\left( {{r}_{238}}-{{r}_{235}} \right)$
Now we need to find the radius of ${{U}^{235}}$ and ${{U}^{238}}$.
We have,
$r=\dfrac{mv}{B}$
Therefore,
$\Rightarrow {{r}_{238}}=\dfrac{mv}{B}$
We know $m=238$ and from earlier calculations we have, $B=\dfrac{v}{10}$. Therefore we get,
$\Rightarrow {{r}_{238}}=\dfrac{238\times v}{\left( \dfrac{v}{10} \right)}$
$\therefore {{r}_{238}}=238\times 10=2380$
Now let us find the radius of ${{U}^{235}}$.
$\Rightarrow {{r}_{235}}=\dfrac{mv}{B}$
We have $m=235$ and $B=\dfrac{v}{10}$. Therefore,
$\Rightarrow {{r}_{235}}=\dfrac{235\times v}{\left( \dfrac{v}{10} \right)}$
$\Rightarrow {{r}_{235}}=235\times 10=2350$
Therefore we can calculate the separation between ${{U}^{235}}$ and ${{U}^{238}}$.
$\Rightarrow S=2\left( 2380-2350 \right)$
$\Rightarrow S=2\times 30$
$\therefore S=60mm$
Thus we get the distance between ${{U}^{235}}$ and ${{U}^{238}}$as 60 mm.
Hence the correct answer is option A.

Note:
Here we take the velocity of all the charged particles as ‘$v$’. This is because it is said in the question, that we pass the particles, one by one into the velocity selector. So after entering the velocity selector, we know that the velocities of all the particles will be the same.