Question
Question: $\prod_{n=1}^{k}(1+x^n)^n$...
∏n=1k(1+xn)n
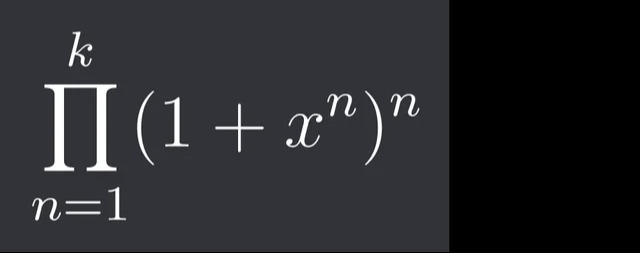
∏n=1k(1+xn)n
Solution
The given expression is a product:
∏n=1k(1+xn)n
This notation means we multiply terms of the form (1+xn)n for each integer value of n from 1 to k.
Let's write out the terms of the product:
For n=1, the term is (1+x1)1=(1+x).
For n=2, the term is (1+x2)2.
For n=3, the term is (1+x3)3.
...
For n=k, the term is (1+xk)k.
So, the product can be written as:
(1+x)1⋅(1+x2)2⋅(1+x3)3⋅…⋅(1+xk)k
This expression represents a polynomial in x if k is a positive integer. For example:
- If k=1, the product is (1+x).
- If k=2, the product is (1+x)(1+x2)2=(1+x)(1+2x2+x4)=1+x+2x2+2x3+x4+x5.
This type of product does not simplify into a common closed-form expression using standard mathematical identities or formulas. The terms in the product, (1+xn)n, are distinct for different values of n and do not exhibit a pattern that allows for cancellation (like in telescoping products) or combination into a simpler form (like in geometric series products).
Therefore, the given expression is already in its most compact and general form. There is no simpler algebraic closed-form solution for this product for arbitrary k and x.
The expression itself is the 'solution' in the sense that it's the most simplified and general representation of the product.
