Question

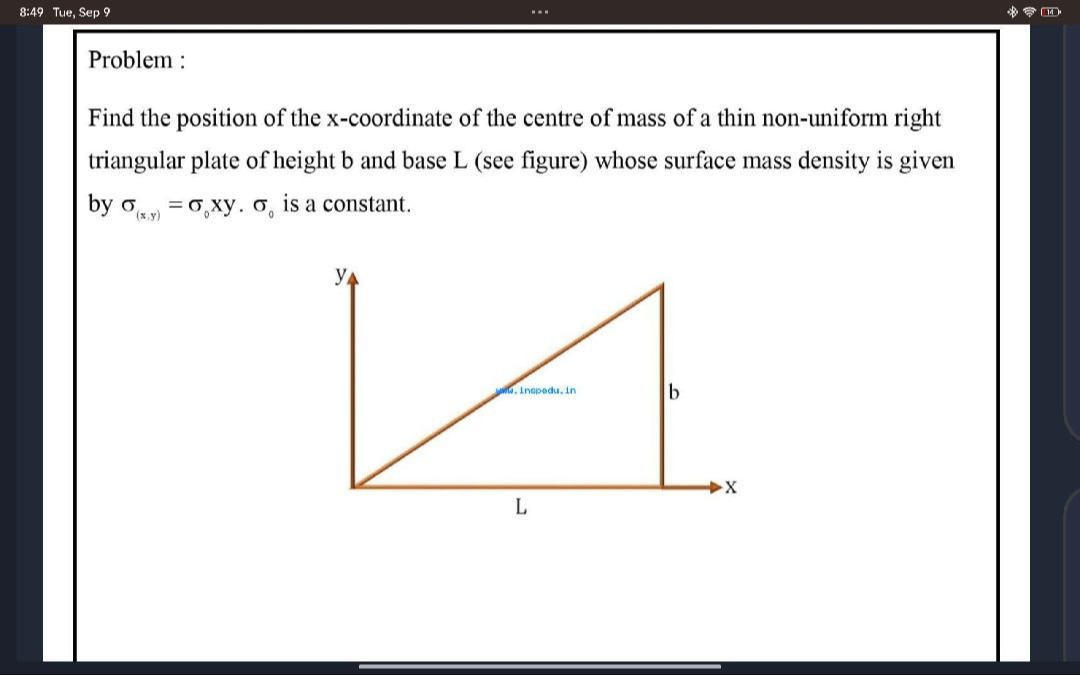
Find the position of the x-coordinate of the centre of mass of a thin non-uniform right triangular plate of height b and base L (see figure) whose surface mass density is given by $\sigma_{(x,y)} = \sigma_0 xy$. $\sigma_0$ is a constant.

• A. $\frac{L}{3}$
• B. $\frac{2L}{5}$
• C. $\frac{L}{2}$
• D. $\frac{3L}{5}$

Answer 1

Answer: (B)

$\frac{2L}{5}$

Answer 2

The x-coordinate of the center of mass ($X_{CM}$) is given by $X_{CM} = \frac{\int x \, dm}{\int dm}$, where $dm = \sigma \, dA$ is the mass of an infinitesimal area element $dA$, and $\sigma$ is the surface mass density. The triangular plate is defined by the vertices (0,0), (L,0), and (0,b). The equation of the hypotenuse is $y = b(1 - x/L)$. The surface mass density is given by $\sigma(x,y) = \sigma_0 xy$.

We can set up the integrals over the area of the triangle. For an element $dA = dx \, dy$, the limits of integration are $0 \le x \le L$ and $0 \le y \le b(1 - x/L)$.

1. Calculate the total mass (M): $M = \iint_A \sigma \, dA = \int_{0}^{L} \int_{0}^{b(1 - x/L)} \sigma_0 xy \, dy \, dx$ First, integrate with respect to y: $\int_{0}^{b(1 - x/L)} \sigma_0 xy \, dy = \sigma_0 x \left[ \frac{y^2}{2} \right]_{0}^{b(1 - x/L)} = \sigma_0 x \frac{b^2}{2} \left(1 - \frac{x}{L}\right)^2$ Now, integrate with respect to x: $M = \int_{0}^{L} \sigma_0 \frac{b^2}{2} x \left(1 - \frac{x}{L}\right)^2 \, dx$ Let $u = 1 - x/L$, so $x = L(1-u)$ and $dx = -L \, du$. When $x=0$, $u=1$; when $x=L$, $u=0$. $M = \sigma_0 \frac{b^2 L^2}{2} \int_{1}^{0} (1-u) u^2 (-du) = \sigma_0 \frac{b^2 L^2}{2} \int_{0}^{1} (u^2 - u^3) \, du$ $M = \sigma_0 \frac{b^2 L^2}{2} \left[ \frac{u^3}{3} - \frac{u^4}{4} \right]_{0}^{1} = \sigma_0 \frac{b^2 L^2}{2} \left(\frac{1}{3} - \frac{1}{4}\right) = \sigma_0 \frac{b^2 L^2}{24}$

2. Calculate the moment about the y-axis ($\int x \, dm$): $\int x \, dm = \iint_A x \sigma \, dA = \int_{0}^{L} \int_{0}^{b(1 - x/L)} x (\sigma_0 xy) \, dy \, dx$ $= \int_{0}^{L} \sigma_0 x^2 \int_{0}^{b(1 - x/L)} y \, dy \, dx$ First, integrate with respect to y: $\int_{0}^{b(1 - x/L)} y \, dy = \left[ \frac{y^2}{2} \right]_{0}^{b(1 - x/L)} = \frac{b^2}{2} \left(1 - \frac{x}{L}\right)^2$ Now, integrate with respect to x: $\int x \, dm = \int_{0}^{L} \sigma_0 x^2 \frac{b^2}{2} \left(1 - \frac{x}{L}\right)^2 \, dx$ Using the substitution $u = 1 - x/L$: $\int x \, dm = \sigma_0 \frac{b^2 L^3}{2} \int_{0}^{1} (1-u)^2 u^2 \, du = \sigma_0 \frac{b^2 L^3}{2} \int_{0}^{1} (u^2 - 2u^3 + u^4) \, du$ $\int x \, dm = \sigma_0 \frac{b^2 L^3}{2} \left[ \frac{u^3}{3} - \frac{2u^4}{4} + \frac{u^5}{5} \right]_{0}^{1} = \sigma_0 \frac{b^2 L^3}{2} \left(\frac{1}{3} - \frac{1}{2} + \frac{1}{5}\right)$ $\int x \, dm = \sigma_0 \frac{b^2 L^3}{2} \left(\frac{10 - 15 + 6}{30}\right) = \sigma_0 \frac{b^2 L^3}{60}$

3. Calculate $X_{CM}$: $X_{CM} = \frac{\int x \, dm}{M} = \frac{\sigma_0 \frac{b^2 L^3}{60}}{\sigma_0 \frac{b^2 L^2}{24}} = \frac{L^3}{60} \times \frac{24}{L^2} = \frac{24L}{60} = \frac{2L}{5}$