Question
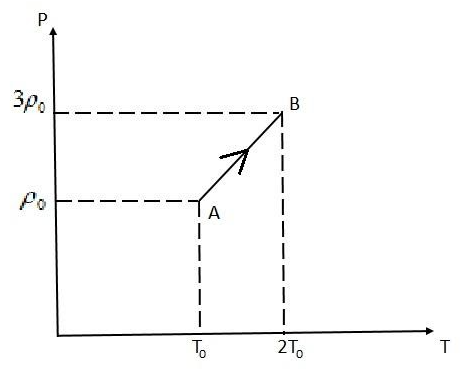
Question: Pressure versus temperature graph of an ideal gas as shown in figure. Density of the gas at point A ...
Pressure versus temperature graph of an ideal gas as shown in figure. Density of the gas at point A is ρ0. Density of point B will be:
A. 43ρ0
B. 23ρ0
C. 34ρ0
D. 34ρ0
Solution
In this question, first of all observe the given graph carefully to write the sufficient and to get a clear idea of what we have to find. Then using the empirical form of ideal gas and the formulae of density and kinetic theory of gas we get the required answer.
Formulae Used:
1. ρ=vm
2. v=ργP
Complete answer:
The ideal gas law is also known as the general gas equation. It is the equation of state of a hypothetical ideal gas. The ideal gas law in empirical form is: PV=NRT.
Since we are given that Density of the gas at point A is ρ0.
As we know that the ideal gas law in empirical form is: PV=NRT
Where P, V and T are the pressure, volume and temperature.
And N is the substance equal to total mass of the gas (m) divided by the molar mass (M)
R is the ideal gas constant.
Now by replacing N with Mm, and subsequently introducing density by ρ=vm we get,
PV=MmRT
Or RTPM=ρ
Also, we know that kinetic theory of gas is-
v=ργP
From this, we are clear that the velocity of the sound in the gas is proportional to T and P where ρ is constant.
So, we can conclude that
ρ is proportional to TP.
In this ideal gas case at points A and B, (ρA=(TP)A) and (ρB=(TP)B)
Dividing both of them, we get
ρBρA=(TP)B(TP)A
Here we have (TP)A=Toρo and l(TP)B=2To3ρo
So, we have
By cross-multiplying, we get
⇒3ρA=2ρB ⇒23ρA=ρBWe conclude at point B, density will be
ρB=23ρo [∵ρA=ρo]
Therefore, the correct option is B. 23ρ0
Note: In this question, we must know that kinetic theory of gas is a historically significant model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. Also, one must be clear that (N) is calculated by dividing total mass of the gas (m) to the molar mass (M) in the ideal gas law i.e., PV=NRT.
