Question

The graph shows variation of I with f for a series R-L-C network. Keeping L and C constant. If R decreases:

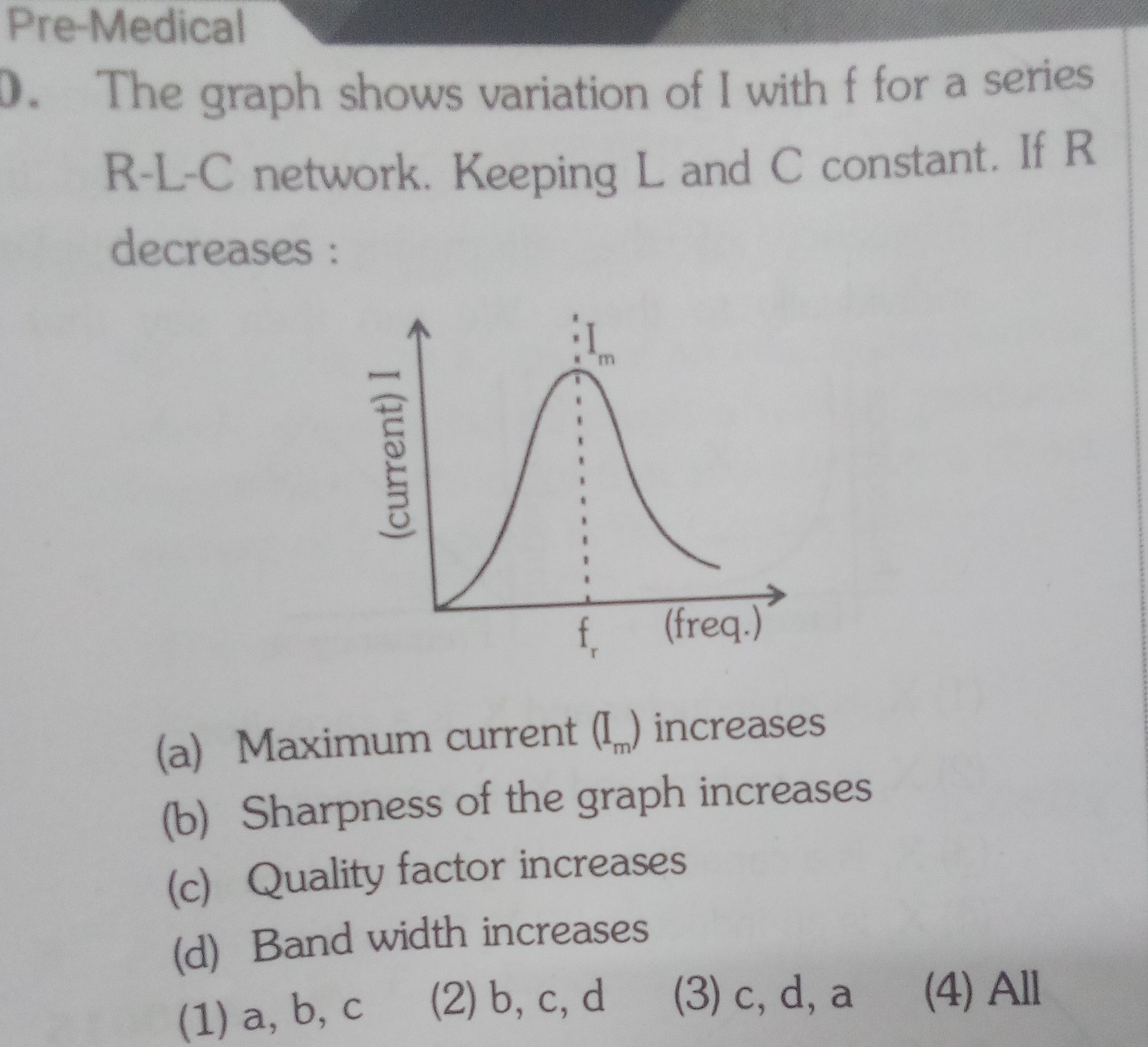
• A. Maximum current ($I_m$) increases
• B. Sharpness of the graph increases
• C. Quality factor increases
• D. Band width increases

Answer 1

Answer: (A), (B), (C)

(1) a, b, c

Answer 2

The problem asks us to analyze the effect of decreasing resistance (R) in a series R-L-C network, while keeping inductance (L) and capacitance (C) constant, on various parameters related to the current (I) versus frequency (f) graph.

1. Maximum current ($I_m$): In a series R-L-C circuit, the current is given by $I = \frac{V}{Z}$, where $V$ is the applied voltage and $Z$ is the impedance. The impedance is $Z = \sqrt{R^2 + (X_L - X_C)^2}$, where $X_L = 2\pi f L$ is the inductive reactance and $X_C = \frac{1}{2\pi f C}$ is the capacitive reactance. Maximum current occurs at resonance, where $X_L = X_C$. At resonance, the impedance is minimum and equal to $R$. So, the maximum current is $I_m = \frac{V}{R}$. If R decreases, and V is constant, then $I_m$ will increase. Therefore, statement (a) is correct.

2. Sharpness of the graph: The sharpness of the resonance curve describes how quickly the current falls off from its maximum value as the frequency deviates from the resonant frequency. A sharper graph means a narrower band of frequencies around resonance where the current is significantly high. This is directly related to the quality factor (Q-factor) and inversely related to the bandwidth. As we will see in points (c) and (d), when R decreases, the Q-factor increases and the bandwidth decreases. Both of these effects lead to an increase in the sharpness of the resonance curve. Therefore, statement (b) is correct.

3. Quality factor (Q-factor): The quality factor (Q-factor) for a series R-L-C circuit at resonance is given by: $Q = \frac{\omega_r L}{R} = \frac{1}{R}\sqrt{\frac{L}{C}}$ Since L and C are kept constant, and R decreases, the Q-factor will increase. A higher Q-factor implies a sharper resonance. Therefore, statement (c) is correct.

4. Bandwidth: The bandwidth ($\Delta f$) of a series R-L-C circuit is the range of frequencies over which the power dissipated in the circuit is at least half of the maximum power (or current is at least $1/\sqrt{2}$ times the maximum current). It is given by: $\Delta f = \frac{R}{2\pi L}$ Alternatively, it is related to the resonant frequency ($f_r$) and Q-factor by: $Q = \frac{f_r}{\Delta f} \implies \Delta f = \frac{f_r}{Q}$ The resonant frequency $f_r = \frac{1}{2\pi\sqrt{LC}}$ remains constant as L and C are constant. If R decreases, then from $\Delta f = \frac{R}{2\pi L}$, the bandwidth $\Delta f$ will decrease. Also, since Q increases (from point c) and $f_r$ is constant, $\Delta f = \frac{f_r}{Q}$ will decrease. Therefore, statement (d) "Band width increases" is incorrect. Bandwidth decreases.

Based on the analysis, statements (a), (b), and (c) are correct.