Question

PQRS is a square. A, B, C, D are points on $\overline {PQ}$ ,$\overline {QR}$ , $\overline {RS}$ and $\overline {SP}$ respectively such that $AP = BQ = CR = DS$ . Prove: $B{D^2} = 2A{D^2} = 2\left( {A{P^2} + A{Q^2}} \right)$

Answer 1

We can draw the diagram. Using the congruency of triangles, we can prove that the line joining the points on the sides of the square are equal. Then we can prove that the angles formed by joining the points A, B, C, D are $90^\circ$. Then we can apply the Pythagoras theorem in the bigger triangle and give proper substitution to get the 1st part of the relation. For the 2nd part, we can apply the Pythagoras theorem in the smaller triangle and by giving suitable substitutions.

Complete step by step answer:

We can draw a diagram with the given details.

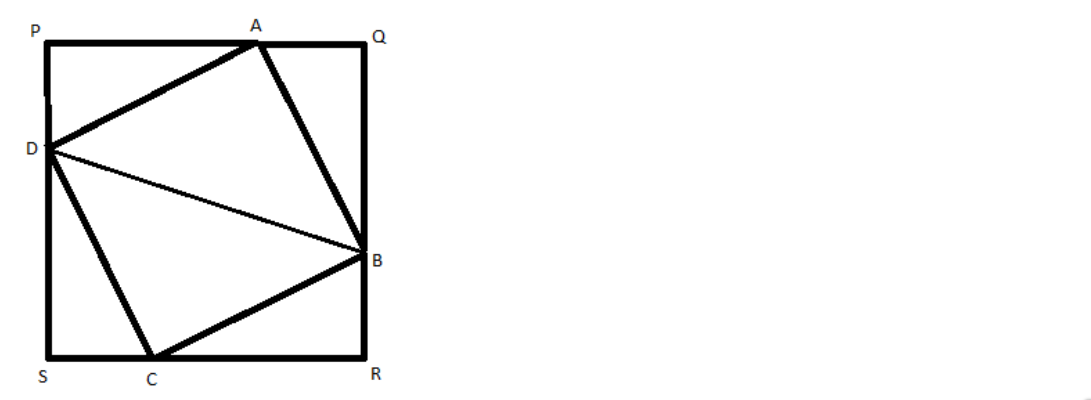
Let us consider the triangles APD and BQA
It is given that $AP = BQ$ … (1)
As PQRS is a square, all the sides are equal and all the angles will be equal to $90^\circ$
$\Rightarrow \angle APD = \angle BQA = 90^\circ$ … (2)
As PQ and PS are sides of the square, they will be equal.
$\Rightarrow PQ = PS$
As A and D are points on PQ and PS, we can write,
$\Rightarrow PA + AQ = PD + DS$
It is given in the question that $AP = DS$
$\Rightarrow AQ = PD$.. (3)
From (1), (2), and (3), the 2 sides and the angle between them are equal.
So, by SAS congruence criteria, the triangles APD and BQA are congruent.
We know that corresponding angles and sides of congruent triangles will be equal.
$\Rightarrow AD = AB$ … (4)
$\Rightarrow \angle PDA = \angle QAB$ … (6)
Consider the triangle APD,
By angle sum property, the sum of the interior angles of a triangle will be equal to $180^\circ$
$\Rightarrow \angle PAD + \angle ADP + \angle APD = 180^\circ$
On substituting equation (2), we get,
$\Rightarrow \angle PAD + \angle ADP + 90^\circ = 180^\circ$
On simplification, we get,
$\Rightarrow \angle PAD + \angle ADP = 90^\circ$ … (7)
Let us now consider the angles on the line PQ, $\angle PAD$, $\angle QAB$, and $\angle DAB$. As they are angles on a straight line, their sum will be $180^\circ$.
$\Rightarrow \angle PAD + \angle QAB + \angle DAB = 180^\circ$
On substituting equation (6), we get,
$\Rightarrow \angle PAD + \angle PDA + \angle DAB = 180^\circ$
Now we can substitute equation (7).
$\Rightarrow 90^\circ + \angle DAB = 180^\circ$
On subtracting $90^\circ$ from both sides, we get,
$\Rightarrow \angle DAB = 90^\circ$ … (8)
Now we can consider, the triangle ABD,
From (8), we can say that ABD is a right-angled triangle.
So, we can apply the Pythagoras theorem.
According to the Pythagoras theorem, the sum of the squares of the non-hypotenuse sides is equal to the square of the hypotenuse.
$\Rightarrow B{D^2} = A{D^2} + A{B^2}$
On substituting equation (4), we get,
$\Rightarrow B{D^2} = A{D^2} + A{D^2}$
$\Rightarrow B{D^2} = 2A{D^2}$ … (9)
Now consider right-angled triangle APD right-angled at P.
We can use the Pythagoras theorem.
$\Rightarrow A{D^2} = P{D^2} + A{P^2}$
On substituting equation (3), we get,
$\Rightarrow A{D^2} = A{Q^2} + A{P^2}$ … (10)
Now we can substitute equation (10) in (9).
$\Rightarrow B{D^2} = 2A{D^2} = 2\left( {A{P^2} + A{Q^2}} \right)$
Thus, we have proved the required relation.

Note: The most important concept used here is the congruency of triangles. 2 triangles are congruent if they can be superimposed on each other. If 2 triangles are congruent, their corresponding angles and sides will be equal. Another important theorem used is the Pythagoras theorem. It is valid only for right-angled triangles only. We cannot simply conclude that $\angle DAB$ is a right angle. We must prove that using the concept of angles on a line and angle sum property of a triangle and suitable substitution.