Question

PQRS is a parallelogram. The position vectors of P, Q R and S in order are, respectively, $\vec{p}=-3\hat{k}$, $\vec{q}=\hat{i}+y\hat{j}$, $\vec{r}=5\hat{i}+2x\hat{j}+\hat{k}$ and $\vec{s}=y\hat{i}-2\hat{k}$ The values of $x$ and $y$ are

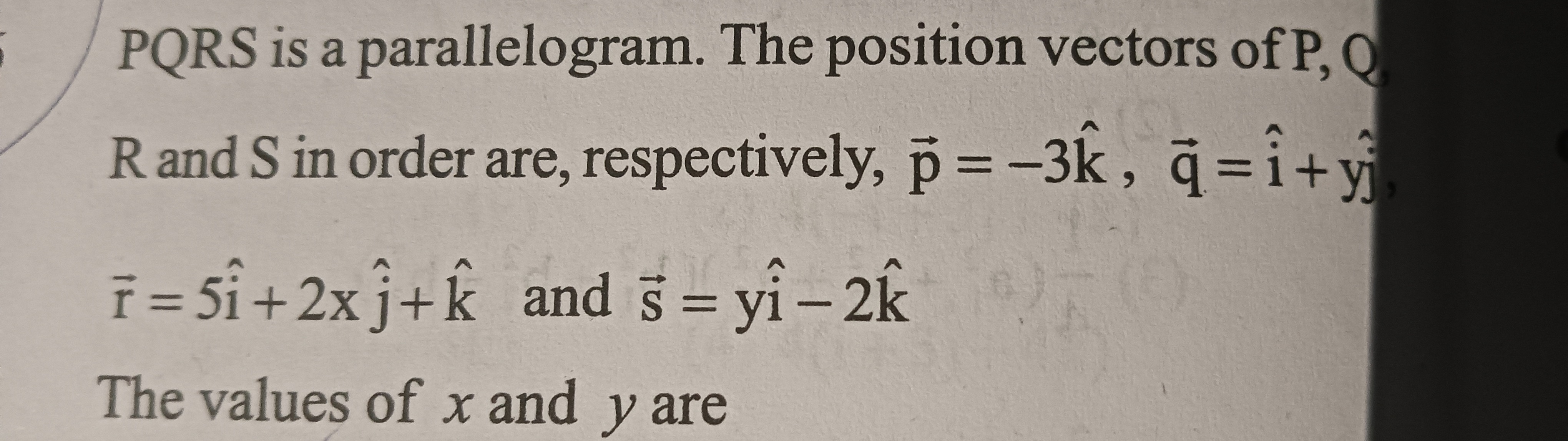
Answer 1

x = 2, y = 4

Answer 2

In a parallelogram, the diagonals bisect each other. Therefore, the midpoint of $PR$ equals the midpoint of $QS$. This gives:

$$\vec{P} + \vec{R} = \vec{Q} + \vec{S}.$$

Given:

$$\vec{P} = -3\hat{k},\quad \vec{Q} = \hat{i} + y\hat{j},\quad \vec{R} = 5\hat{i} + 2x\hat{j} + \hat{k},\quad \vec{S} = y\hat{i} - 2\hat{k}.$$

Calculate:

$$\vec{P} + \vec{R} = (-3\hat{k}) + (5\hat{i} + 2x\hat{j} + \hat{k}) = 5\hat{i} + 2x\hat{j} - 2\hat{k},$$ $$\vec{Q} + \vec{S} = (\hat{i} + y\hat{j}) + (y\hat{i} - 2\hat{k}) = (1+y)\hat{i} + y\hat{j} - 2\hat{k}.$$

Equate components:

• i-component:

$$5 = 1 + y \quad \Rightarrow \quad y = 4.$$

• j-component:

$$2x = y \quad \Rightarrow \quad 2x = 4 \quad \Rightarrow \quad x = 2.$$

• k-component:

$$-2 = -2 \quad (\text{automatically satisfied}).$$