Question

PQ is double ordinate of hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ such that OPQ is an equilateral triangle, O being the center of hyperbola, where the eccentricity of the hyperbola $e$ satisfy,$\sqrt 3 e > k$, then the value of k is

Answer 1

Here we have to find the value of eccentricity of the hyperbola. We will first write the polar coordinates of the point P and point Q. Here it is given that the OPQ is an equilateral triangle. O is the center of the hyperbola; all the angles of the triangle will be $60^\circ$. Then we will apply the distance formula and eccentricity formula for hyperbola to get the value of k.

Complete step-by-step answer:
We will draw the figure first with appropriate data given.

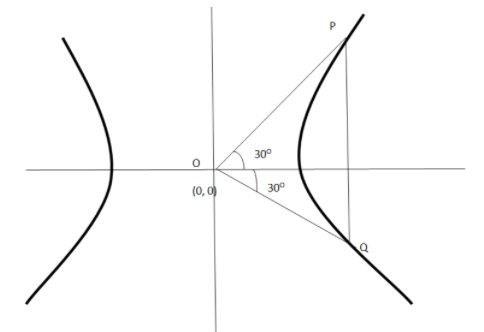
It is given that O is the center of the hyperbola and PQ is the double ordinate of the hyperbola. So the coordinate of point P $= \left( {a\sec \theta ,b\tan \theta } \right)$ and coordinate of Q $= \left( {a\sec \theta , - b\tan \theta } \right)$
Since $\Delta POQ$ is an equilateral triangle. So the length of all sides is equal. Thus, $PO = QO = PQ$.
We will find the distance between these two points, $\left( {a\sec \theta , - b\tan \theta } \right)$ and $\left( {a\sec \theta ,b\tan \theta } \right)$.
Now we will replace ${x_1}$ with $a\sec \theta$, ${y_1}$ with $- b\tan \theta$, ${x_2}$ with $a\sec \theta$ and ${y_2}$ with $b\tan \theta$ in the distance formula $\sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]}$.
Distance of the point $\left( {a\sec \theta , - b\tan \theta } \right)$ from \left( {a\sec \theta ,b\tan \theta } \right)$$$$ = \sqrt {\left[ {{{\left( {a\sec \theta - a\sec \theta } \right)}^2} + {{\left( {b\tan \theta - ( - b\tan \theta )} \right)}^2}} \right]}
Subtracting the terms and applying exponents on the bases, we get
Distance of the point $\left( {a\sec \theta , - b\tan \theta } \right)$from $\left( {a\sec \theta ,b\tan \theta } \right)$ $= \sqrt {0 + 4{b^2}{{\tan }^2}\theta }$ …………..$\left( 1 \right)$
Similarly, we will find the distance between the points $\left( {0,0} \right)$ and $\left( {a\sec \theta ,b\tan \theta } \right)$.
Now we will replace ${x_1}$ with 0, ${y_1}$ with 0, ${x_2}$ with $a\sec \theta$ and ${y_2}$ with $b\tan \theta$ in the distance formula $\sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]}$.
Distance of the point $\left( {0,0} \right)$ from $\left( {a\sec \theta ,b\tan \theta } \right)$ $= \sqrt {\left[ {{{\left( {a\sec \theta - 0} \right)}^2} + {{\left( {b\tan \theta - 0} \right)}^2}} \right]}$
Applying exponents on the bases, we get
Distance of point $\left( {0,0} \right)$ from $\left( {a\sec \theta ,b\tan \theta } \right)$ $= \sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}\theta }$………….$\left( 2 \right)$
Squaring and equating equation $\left( 1 \right)$ and equation $\left( 2 \right)$, we get
${\left( {\sqrt {0 + 4{b^2}{{\tan }^2}\theta } } \right)^2} = {\left( {\sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}\theta } } \right)^2}$
Simplifying the equation, we get
$\Rightarrow$ $4{a^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta + {a^2}{\tan ^2}\theta$
Adding and subtracting like terms, we get
$\Rightarrow$ $3{b^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta$
On further simplification, we get
$\Rightarrow$ $\dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{{{\sec }^2}\theta }}{{3{{\tan }^2}\theta }}$
Breaking the terms, we get
$\Rightarrow$ $\dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{\dfrac{1}{{{{\cos }^2}\theta }}}}{{\dfrac{{3{{\sin }^2}\theta }}{{{{\cos }^2}\theta }}}} = \dfrac{1}{{3{{\sin }^2}\theta }}$
We know the square of eccentricity of hyperbola is equal to $1 + \dfrac{{{b^2}}}{{{a^2}}}$ i.e. ${e^2} = 1 + \dfrac{{{b^2}}}{{{a^2}}}$
We will put the value of $\dfrac{{{b^2}}}{{{a^2}}}$ that we have calculated, in the above formula.
$\Rightarrow$ ${e^2} = 1 + \dfrac{1}{{3{{\sin }^2}\theta }}$
Simplifying the terms further, we get
$\Rightarrow$ ${e^2} = \dfrac{{1 + 4{{\tan }^2}\theta }}{{3{{\tan }^2}\theta }}$
Rewriting the equation, we get
$\Rightarrow$ $\dfrac{1}{{3\left( {{e^2} - 1} \right)}} = {\sin ^2}\theta$
We know that ${\sin ^2}\theta < 1$.
Therefore,
$\Rightarrow$ $\dfrac{1}{{3\left( {{e^2} - 1} \right)}} < 1$
Using inequality property, we get
$\Rightarrow$ $3\left( {{e^2} - 1} \right) > 1$
Simplifying the terms, we get
$\Rightarrow$ ${e^2} - 1 > \dfrac{1}{3}$
Adding 1 on both sides, we get
$\Rightarrow {e^2} - 1 + 1 > \dfrac{1}{3} + 1\\\ \Rightarrow {e^2} > \dfrac{4}{3}$
Taking square root on both sides, we get
$\Rightarrow \sqrt {{e^2}} > \sqrt {\dfrac{4}{3}} \\\\\Rightarrow e > \dfrac{2}{{\sqrt 3 }}\\\\\Rightarrow \sqrt 3 e > 2$
Thus, the value of $k$ is 2.

Note: We have found out the required answer using the eccentricity of hyperbola. Eccentricity is a measure that tells how much a conic section differs from being circular. Conic section includes the circle, hyperbola, parabola etc. Different conic sections have different eccentricity. For example, a circle has an eccentricity 0 whereas hyperbola has an eccentricity usually greater than 1. It therefore becomes very important to keep in mind the formula of eccentricity for different conic sections.