Solveeit Logo
Login

Question

Question: PQ is a post of height \(a\), and A is a tower at some distance; \(\alpha \)and \(\beta \) are the a...

PQ is a post of height aa, and A is a tower at some distance; α\alpha and β\beta are the angles of elevation of B, the top of tower, at P and Q respectively. The height of the tower is

A. asin⁡αcos⁡βsin⁡(α−β){\text{A}}{\text{. }}\dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}}
B. acos⁡αcos⁡βsin⁡(α−β){\text{B}}{\text{. }}\dfrac{{a\cos \alpha \cos \beta }}{{\sin (\alpha - \beta )}}
C. asin⁡αsin⁡βsin⁡(α−β){\text{C}}{\text{. }}\dfrac{{a\sin \alpha \sin \beta }}{{\sin (\alpha - \beta )}}
D.{\text{D}}{\text{.}} None of these

Explanation

Solution

Hint: Draw the figure according to the information provided in the question and they analyse it to solve the question.

Complete step-by-step answer:

According to the question, PQ is a post of height a, and AB is the tower.
Let us assume the height of the tower be h.
The figure for the above question is shown below-


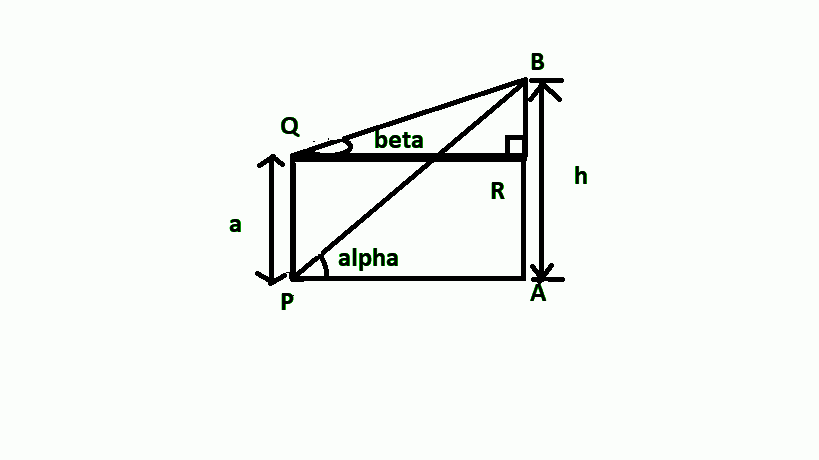
From the figure we can see,
PQ = AR = a.
Therefore, we can also say that, BR = AB -AR – (1)
Now, we know, AB = h (assume)
Therefore, substituting AB = h and AR = a in equation (1), we get-
BR=h−a−(2)BR = h - a - (2)
Now, in right angled triangle BAP,
tan⁡α=ABAP ∴tan⁡α=hAP ⇒AP=htan⁡α−(3)  \tan \alpha = \dfrac{{AB}}{{AP}} \\\ \therefore \tan \alpha = \dfrac{h}{{AP}} \\\ \Rightarrow AP = \dfrac{h}{{\tan \alpha }} - (3) \\\

Also, in right angle triangle BRQ,
tan⁡β=BRQR ∴tan⁡β=h−aAP[∵AP=RQ] ⇒AP=h−atan⁡β−(4)  \tan \beta = \dfrac{{BR}}{{QR}} \\\ \therefore \tan \beta = \dfrac{{h - a}}{{AP}}[\because AP = RQ] \\\ \Rightarrow AP = \dfrac{{h - a}}{{\tan \beta }} - (4) \\\

From equation (3) and (4), we can say,
h−atan⁡β=htan⁡α ⇒htan⁡α−atan⁡α=htan⁡β ⇒h(tan⁡α−tan⁡β)=atan⁡α ⇒h=atan⁡αtan⁡α−tan⁡β  \dfrac{{h - a}}{{\tan \beta }} = \dfrac{h}{{\tan \alpha }} \\\ \Rightarrow h\tan \alpha - a\tan \alpha = h\tan \beta \\\ \Rightarrow h(\tan \alpha - \tan \beta ) = a\tan \alpha \\\ \Rightarrow h = \dfrac{{a\tan \alpha }}{{\tan \alpha - \tan \beta }} \\\

We can write, tan⁡α=sin⁡αcos⁡α,tan⁡β=sin⁡βcos⁡β\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }},\tan \beta = \dfrac{{\sin \beta }}{{\cos \beta }}

So, h will be equal to, h=asin⁡αcos⁡αsin⁡αcos⁡α−sin⁡βcos⁡β=asin⁡αcos⁡α×cos⁡αcos⁡βsin⁡αcos⁡β−cos⁡αsin⁡β ⇒h=asin⁡αcos⁡βsin⁡(α−β)  h = \dfrac{{a\dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - \dfrac{{\sin \beta }}{{\cos \beta }}}} = a\dfrac{{\sin \alpha }}{{\cos \alpha }} \times \dfrac{{\cos \alpha \cos \beta }}{{\sin \alpha \cos \beta - \cos \alpha \sin \beta }} \\\ \Rightarrow h = \dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}} \\\

Hence, the height of the tower is, h=asin⁡αcos⁡βsin⁡(α−β)h = \dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}}.
Therefore, the correct option is A.

Note- Whenever such types of questions appear, always write the information given in the question, and using that make a figure, find the value of the tangent of angle α,β\alpha ,\beta , and then solve further by making required substitutions.