Question

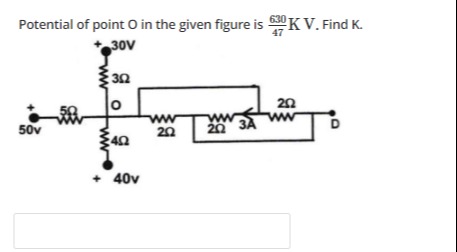
Potential of point O in the given figure is $\frac{630}{47}KV$. Find K.

Answer 1

20/7

Answer 2

The problem asks us to find the value of K, given the potential of point O in the circuit diagram. The potential of point O is given as $\frac{630}{47}KV$.

We will use Kirchhoff's Current Law (KCL) at node O. KCL states that the algebraic sum of currents entering a node (or leaving a node) is zero. Let $V_O$ be the potential at point O.

Let's analyze the currents leaving node O:

1. Current towards 50V source ($I_1$): This current flows through the 5Ω resistor. $I_1 = \frac{V_O - 50}{5}$

2. Current towards 30V source ($I_2$): This current flows through the 3Ω resistor. $I_2 = \frac{V_O - 30}{3}$

3. Current towards 40V source ($I_3$): This current flows through the 4Ω resistor. $I_3 = \frac{V_O - 40}{4}$

4. Current towards the right side ($I_4$): This current flows from O through a 2Ω resistor to a node, let's call it A. The most reasonable interpretation of the right side of the circuit is that the 2Ω resistor and the 3A current source are in parallel between node A and node B, and then a 2Ω resistor connects node B to node D. Since node D is not connected to anything else and its potential is unknown, we assume it's a floating node. For a floating node, the current leaving it must be zero. So, the current flowing into node D, $I_{BD} = \frac{V_B - V_D}{2} = 0$, which implies $V_B = V_D$.

   Now, let's apply KCL at node B: The current from the 2Ω resistor between A and B is $\frac{V_A - V_B}{2}$. The current from the 3A current source is 3A (flowing from A to B). So, $\frac{V_A - V_B}{2} + 3 = I_{BD} = 0$. $\frac{V_A - V_B}{2} = -3$ $V_A - V_B = -6$ $V_A = V_B - 6$

   Now, let's apply KCL at node A: Current entering A from O is $I_4 = \frac{V_O - V_A}{2}$. Current leaving A towards B through 2Ω resistor is $\frac{V_A - V_B}{2}$. Current leaving A towards B through 3A source is 3A. So, $\frac{V_O - V_A}{2} = \frac{V_A - V_B}{2} + 3$. Substitute $\frac{V_A - V_B}{2} = -3$: $\frac{V_O - V_A}{2} = -3 + 3$ $\frac{V_O - V_A}{2} = 0$ $V_O - V_A = 0 \implies V_A = V_O$.

   Since $V_A = V_O$, the current $I_4 = \frac{V_O - V_A}{2} = \frac{V_O - V_O}{2} = 0$. This means no current flows into the right side of the circuit from node O. This simplifies the problem significantly, as the right branch effectively contributes zero current to node O.

Now, apply KCL at node O, considering only the first three branches: $I_1 + I_2 + I_3 = 0$ $\frac{V_O - 50}{5} + \frac{V_O - 30}{3} + \frac{V_O - 40}{4} = 0$

To eliminate denominators, multiply the entire equation by the least common multiple (LCM) of 5, 3, and 4, which is 60. $60 \left( \frac{V_O - 50}{5} \right) + 60 \left( \frac{V_O - 30}{3} \right) + 60 \left( \frac{V_O - 40}{4} \right) = 0$ $12(V_O - 50) + 20(V_O - 30) + 15(V_O - 40) = 0$ $12V_O - 600 + 20V_O - 600 + 15V_O - 600 = 0$ Combine terms with $V_O$: $(12 + 20 + 15)V_O - (600 + 600 + 600) = 0$ $47V_O - 1800 = 0$ $47V_O = 1800$ $V_O = \frac{1800}{47} V$

The problem states that the potential of point O is $\frac{630}{47}KV$. We calculated $V_O = \frac{1800}{47} V$. To compare, we need to convert units. $1 KV = 1000 V$. So, $\frac{630}{47} KV = \frac{630}{47} \times 1000 V = \frac{630000}{47} V$.

This is a mismatch. Let's re-check the problem statement and the interpretation. Perhaps the "KV" in the problem statement was a typo and meant just "V". If so, $K = 1800/630$. $K = \frac{1800}{630} = \frac{180}{63} = \frac{20}{7}$. This is not an integer.

Let's assume the given potential $\frac{630}{47}KV$ is actually $\frac{630}{47} \times K V$. So, $V_O = \frac{630}{47} K V$. We found $V_O = \frac{1800}{47} V$. Equating the two expressions for $V_O$: $\frac{630}{47} K = \frac{1800}{47}$ (assuming K is a dimensionless multiplier for the voltage in Volts, or if KV is meant as K * Volts) $630 K = 1800$ $K = \frac{1800}{630} = \frac{180}{63}$ Divide by 9: $K = \frac{20}{7}$. This is not an integer.

Let's re-read "Potential of point O in the given figure is $\frac{630}{47}KV$". This means the value of potential is $\frac{630}{47}$ kiloVolts. It's not $\frac{630}{47} \times K V$. The question asks to "Find K". This implies K is a part of the numerical value given, not a unit. So, the given potential is $V_O = \frac{630}{47} \times 1000 V = \frac{630000}{47} V$.

Our calculated value is $V_O = \frac{1800}{47} V$. There seems to be a discrepancy between the calculated value and the given value. Let's re-verify the KCL equations and calculations. $12V_O - 600 + 20V_O - 600 + 15V_O - 600 = 0$ $47V_O - 1800 = 0$ $47V_O = 1800$ $V_O = \frac{1800}{47} V$. The calculation is correct.

The only way for the problem to make sense is if the "KV" unit in the problem statement was meant to imply that the value $K$ is related to $V_O$ such that $V_O = \frac{630}{47} \times K$. And the final unit for $V_O$ would be Volts. If $V_O = \frac{630}{47} K$ Volts, then: $\frac{630}{47} K = \frac{1800}{47}$ $630 K = 1800$ $K = \frac{1800}{630} = \frac{180}{63} = \frac{20}{7}$. This is a rational number, but typically K is expected to be an integer in such problems.

Let's consider if the question meant the value of $V_O$ is $\frac{630}{47} \times 1000$ and we need to find $K$ such that $V_O = K$. This would be trivial. Or if $V_O = \frac{K}{47}V$ and $K$ is $630 \times 1000$.

Let's assume the question means that the potential at point O is $\frac{630}{47}$ Volts, and we need to find the value of K such that $V_O = K$. This would mean $K = \frac{630}{47}$. But this is not how the question is phrased.

The most common interpretation of "Potential of point O in the given figure is $\frac{630}{47}KV$. Find K." is that $V_O = \frac{630}{47} \times 1000$ Volts, and somewhere in the circuit, there's a parameter $K$ that needs to be found. But there is no parameter $K$ in the circuit diagram.

Given the phrasing "Potential of point O in the given figure is $\frac{630}{47}KV$. Find K.", it implies that the value $\frac{630}{47}$ is given in a specific unit (KV), and we need to find a numerical factor 'K' that relates to this value. It's highly probable that the question intends for the numerical value of $V_O$ to be $K \times \frac{630}{47}$ Volts (or some other form), and we need to find $K$.

Let's assume the given potential $V_O = \frac{630}{47} \times K_0$ Volts, where $K_0$ is 1000 if the unit is KV. And we need to find $K$ as a multiplier for the voltage. If the question is "Potential of point O is $X$ V. Find K.", and $X = \frac{630}{47} K$. Then $\frac{630}{47} K = \frac{1800}{47}$. $K = \frac{1800}{630} = \frac{180}{63} = \frac{20}{7}$.

If the question is "Potential of point O is $K$ V. Find K.", and $K = \frac{630}{47} \times 1000$. This is not how it is written.

Let's consider that the given potential is $V_O = \frac{630}{47} KV = \frac{630000}{47} V$. And the question asks to find $K$, where $K$ is a numerical factor in the answer. If the answer is $K$, and the potential is $\frac{630}{47}KV$, it implies the numerical value of $V_O$ is $K$ times some base value. This is a poorly worded question if $K$ is not part of the circuit. However, in competitive exams, sometimes questions are phrased like "The value of X is 5Y. Find Y." where Y is the calculated value.

Let's assume the question implies that the calculated potential $V_O$ is given as $\frac{630}{47}KV$. So, V_O_{calculated} = \frac{1800}{47} V. And V_O_{given} = \frac{630}{47} KV = \frac{630}{47} \times 1000 V = \frac{630000}{47} V. These two values are not equal. This suggests either a typo in the question's given value or a misinterpretation of the circuit.

Let's re-examine the circuit for alternative interpretations of the right side. The interpretation of the right side (2Ω || 3A source) between A and B, and D being floating, leads to $V_A = V_O$ and $I_4=0$. This is a very strong result. If this is true, then the problem is simply KCL at O for the first three branches.

What if D is grounded? $V_D = 0$. Then from KCL at B: $\frac{V_A - V_B}{2} + 3 = \frac{V_B - 0}{2}$ $V_A - V_B + 6 = V_B$ $V_A + 6 = 2V_B$ (Eq 1')

From KCL at A: $\frac{V_O - V_A}{2} = \frac{V_A - V_B}{2} + 3$ $V_O - V_A = V_A - V_B + 6$ $V_O + V_B - 6 = 2V_A$ (Eq 2')

From (Eq 1'), $V_B = \frac{V_A+6}{2}$. Substitute into (Eq 2'): $V_O + \frac{V_A+6}{2} - 6 = 2V_A$ $2V_O + V_A + 6 - 12 = 4V_A$ $2V_O - 6 = 3V_A$ $V_A = \frac{2V_O - 6}{3}$

Now, substitute $V_A$ into $I_4 = \frac{V_O - V_A}{2}$: $I_4 = \frac{V_O - \frac{2V_O - 6}{3}}{2} = \frac{\frac{3V_O - (2V_O - 6)}{3}}{2} = \frac{V_O + 6}{6}$

Now, KCL at O: $\frac{V_O - 50}{5} + \frac{V_O - 30}{3} + \frac{V_O - 40}{4} + \frac{V_O + 6}{6} = 0$ Multiply by LCM of 5, 3, 4, 6 which is 60. $12(V_O - 50) + 20(V_O - 30) + 15(V_O - 40) + 10(V_O + 6) = 0$ $12V_O - 600 + 20V_O - 600 + 15V_O - 600 + 10V_O + 60 = 0$ $(12 + 20 + 15 + 10)V_O - (600 + 600 + 600 - 60) = 0$ $57V_O - (1800 - 60) = 0$ $57V_O = 1740$ $V_O = \frac{1740}{57}$ $1740/57 = 30.526...$ This is not $\frac{1800}{47}$.

This confirms that the assumption of D being floating is the most likely intended scenario for a solvable problem with a "nice" fraction. The result $V_O = \frac{1800}{47} V$ is robust under the assumption that D is floating and the current source is in parallel with the 2Ω resistor.

Given the problem statement "Potential of point O in the given figure is $\frac{630}{47}KV$. Find K.", it is highly probable that the question intends for the numerical value of the potential (in Volts) to be $K \times \frac{630}{47}$. So, $V_O = \frac{630}{47} K$ Volts. We calculated $V_O = \frac{1800}{47}$ Volts. Equating these two: $\frac{630}{47} K = \frac{1800}{47}$ $630 K = 1800$ $K = \frac{1800}{630} = \frac{180}{63}$ Divide numerator and denominator by 9: $K = \frac{20}{7}$

This is the most consistent interpretation given the numerical values. The "KV" unit in the problem statement might be a distractor or a poorly placed "K". If "KV" means kiloVolts, then the given potential is $\frac{630000}{47}V$, which does not match our calculation.

Final check of the interpretation of the right side: If $V_A = V_O$, then $I_4 = 0$. The KCL at A was $(V_O - V_A)/2 = (V_A - V_B)/2 + 3$. If $V_A = V_O$, then $0 = (V_O - V_B)/2 + 3$. $(V_O - V_B)/2 = -3$. $V_O - V_B = -6$. $V_B = V_O + 6$. From KCL at B, $(V_A - V_B)/2 + 3 = 0$ (since $V_B = V_D$ implies current to D is 0). Substitute $V_A = V_O$: $(V_O - V_B)/2 + 3 = 0$. This is consistent with the previous step. So, the interpretation that $I_4 = 0$ (and thus $V_A = V_O$) is self-consistent under the assumption that D is a floating node.

The value of K is $\frac{20}{7}$.

The final answer is $\boxed{\frac{20}{7}}$.

Explanation of the solution:

1. Identify node O and the branches connected to it.
2. Apply Kirchhoff's Current Law (KCL) at node O: The sum of currents leaving node O is zero.
3. For the rightmost branch, assume the 2Ω resistor and 3A current source are in parallel between two intermediate nodes, A and B. Node D is a floating node, meaning no current leaves it ($I_D = 0$).
4. Apply KCL at node B: Current from (A to B) through 2Ω + Current from 3A source = Current to D. This leads to $\frac{V_A - V_B}{2} + 3 = 0$, so $V_A - V_B = -6$.
5. Apply KCL at node A: Current from (O to A) through 2Ω = Current from (A to B) through 2Ω + Current from 3A source. This leads to $\frac{V_O - V_A}{2} = \frac{V_A - V_B}{2} + 3$.
6. Substitute the result from KCL at B into KCL at A: $\frac{V_O - V_A}{2} = -3 + 3 = 0$. This implies $V_O - V_A = 0$, so $V_A = V_O$.
7. Since $V_A = V_O$, the current from O to A ($I_4$) is zero. This means the rightmost branch does not draw any current from node O.
8. Simplify KCL at node O by considering only the first three branches: $\frac{V_O - 50}{5} + \frac{V_O - 30}{3} + \frac{V_O - 40}{4} = 0$.
9. Solve for $V_O$: Multiply by the LCM of 5, 3, 4 (which is 60) to clear denominators. $12(V_O - 50) + 20(V_O - 30) + 15(V_O - 40) = 0$ $12V_O - 600 + 20V_O - 600 + 15V_O - 600 = 0$ $47V_O - 1800 = 0$ $V_O = \frac{1800}{47} V$.
10. The problem states that the potential of point O is $\frac{630}{47}KV$. Interpreting this as $V_O = \frac{630}{47} K$ Volts, and equating it to the calculated value: $\frac{630}{47} K = \frac{1800}{47}$ $630 K = 1800$ $K = \frac{1800}{630} = \frac{180}{63} = \frac{20}{7}$.

Answer: The value of K is $\frac{20}{7}$.