Question
Question: Potential of point A is ...
Potential of point A is
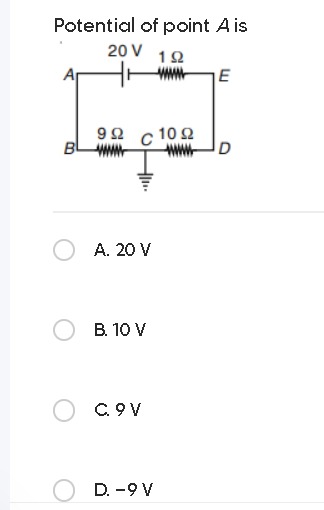
20 V
10 V
9 V
-9 V
9 V
Solution
To find the potential of point A, we first need to interpret the circuit diagram correctly.
-
Identify Ground: Point C is grounded, which means its potential VC=0 V.
-
Identify Connected Nodes:
- The line connecting A and B indicates that points A and B are at the same potential. So, VA=VB.
- The line connecting E and D indicates that points E and D are at the same potential. So, VE=VD.
-
Analyze the 1 Ω Resistor: The 1 Ω resistor is connected between points E and D. Since VE=VD, the potential difference across the 1 Ω resistor is VE−VD=0. Therefore, no current flows through the 1 Ω resistor, and it is effectively shorted (i.e., it behaves like a wire, or it can be removed from the circuit without affecting the currents and voltages in other parts of the circuit).
-
Simplify the Circuit: Let's denote the common potential of A and B as VAB and the common potential of E and D as VED.
- The 20 V battery is connected between A and E. The positive terminal is towards A. So, VA−VE=20 V. This means VAB−VED=20 V.
- The lower branch consists of the 9 Ω resistor and the 10 Ω resistor connected in series between B and D, with point C (grounded) in between. This branch is effectively connected between VAB (at B) and VED (at D).
- The total resistance of this lower branch is Rlower=9Ω+10Ω=19Ω.
-
Calculate the Current: The potential difference across the lower branch (between B and D) is VB−VD. Since VB=VAB and VD=VED, we have VB−VD=VAB−VED=20 V. The current (I) flowing through the lower branch is given by Ohm's Law: I=RlowerVB−VD=19Ω20V=1920 A.
-
Calculate the Potential of Point A: We need to find VA, which is the same as VB. The current I flows from B to C through the 9 Ω resistor. Using Ohm's law for the 9 Ω resistor: VB−VC=I×9Ω We know VC=0 V and I=1920 A. VB−0=(1920)×9 VB=19180 V
Since VA=VB, we have: VA=19180 V
-
Approximate the Value: 19180≈9.47 V.
-
Compare with Options: The calculated value 9.47 V is closest to 9 V among the given options.
