Question

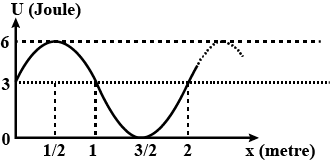
Potential energy (sinusoidal curve) is shown graphically for a particle. The potential energy does not depend on $Y$ and $z$ . For range $0 < X < 2$ ; maximum value of conservative force is $\beta \pi$ (in magnitude). The value of $\beta$ is: (Here the force is corresponding to above potential energy and all units are in $S.I.$ )

Answer 1

In order to solve this question, we are going to firstly analyze the graph and obtain an expression for the potential energy variation with the displacement. Then, after simplifying it, we can find the force expression by partially differentiating the potential energy and then finally finding the maximum.
The propagation constant, $k$ can be written as
$k = \dfrac{{2\pi }}{\lambda }$
Force is expressed as:
$F = - \dfrac{{\delta U}}{{\delta x}}$

Complete step by step solution:
From the graph as given in the question, we can see that the potential energy relation in terms of displacement $x$ can be expressed as:
$U = 3 + 3\sin kx$
Now as we know that the propagation constant, $k$ can be written as
$k = \dfrac{{2\pi }}{\lambda }$
If we take the wavelength to be $2$ in the suitable units, then,
$k = \dfrac{{2\pi }}{2} = \pi$
Therefore, $U = 3 + 3\sin \pi x$
Now as we know that the force is obtained as the negative derivative of potential energy with respect to the displacement $x$ , thus,
$F = - \dfrac{{\delta U}}{{\delta x}} = - 3\pi \cos \pi x$
Now, the force is maximum when,
$\cos \pi x = - 1$
Which gives us the value of the maximum force as:
$\therefore {F_{\max }} = 3\pi$
Thus, as it is given that $\beta \pi$ is the value for the corresponding force, then the value of $\beta$ is $3$ .

Note :
It is important to note that the potential energy is the energy held by an object because of its position relative to the other objects. The maximum force depends upon the change in the potential difference with respect to time. The maxima and the minima of the potential energy are occurring at displacements $\dfrac{1}{2}m$ and $\dfrac{3}{2}m$ .