Question

Potential due to an electric dipole is represented by:
(where $p$ is the dipole moment, $r\left( { \gg 2a} \right)$ is the distance at which the potential V of the dipole is calculated and $\theta$ is the angle between the distance vector and the dipole.)
A. $V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _0}{r^4}}}$
B. $V = \dfrac{{p\sin \theta }}{{4\pi {\varepsilon _0}{r^2}}}$
C. $V = \dfrac{{p\sin \theta }}{{4\pi {\varepsilon _0}{r^4}}}$
D. $V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _0}{r^2}}}$

Answer 1

We knew that there are two types of dipole in nature: electric dipole and the magnetic dipole. Magnetic dipole is a closed system while electric dipole is a system made up of two opposite charges separated by small distances. Electric potential experienced by the dipole at any point is the algebraic sum of potential created by both the positive and negative charges.

Complete answer:
Electric potential is the amount of work required for moving a positive unit charge from the infinite to a specific point inside the electric field. So the electric potential at the point which is at the distance $r$ from the point charge $q$ is as given below:
$V = \dfrac{q}{{4\pi {\varepsilon _0}r}}$, where ${\varepsilon _0}$ is the permittivity of the vacuum or free space.
The electric potential is the scalar quantity. For the system of charged particles, electric potential at the point is the sum of all the potential by the charges. So net potential at the point is:
${V_{net}} = \sum\limits_i^{} {{V_i}}$ $\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}}}\sum\limits_i^{} {\dfrac{{{q_i}}}{{{r_i}}}}$

So for the electric dipole,

                        ![](https://www.vedantu.com/question-sets/e67b2a2c-311f-4e40-a1af-c78bf3e305f68192424233533154733.png)   

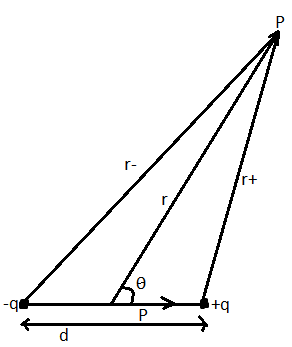
where $p$ is the dipole moment, $r\left( { \gg d} \right)$ is the distance at which the potential V of the dipole is calculated and $\theta$ is the angle between the distance vector and the dipole then,
$V = \dfrac{q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{1}{{{r_ + }}} - \dfrac{1}{{{r_ - }}}} \right) = \dfrac{q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{{r_ - } - {r_ + }}}{{{r_ + }{r_ - }}}} \right)$
Because point p is very far from the dipole so, we can write the electric potential after solving the above equation as: $V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _0}{r^2}}}$ where $p$ dipole moment.

So, the correct answer is “Option D”.

Note:
If the angle between the direction of the dipole to the point at which the electric potential to be calculated is, if $\theta = {90^0}$, then the electric potential at the point is zero and if the angle is $\theta = {0^0}$ then, the electric potential is $V = \dfrac{p}{{4\pi {\varepsilon _0}{r^2}}}$ .