Question

Potassium crystallize in body-centered cubic lattice with the edge length an equal to${\text{5}}{\text{.2}}\,{{\text{A}}^{\text{o}}}$, then what is the distance (in${{\text{A}}^{\text{o}}}$) between nearest neighbours?
A. $2.25$
B.$3.0$
C.$2.5$
D. none of the above

Answer 1

In case of body-centered cubic unit cell, the one-fourth of diagonal length represents the radius. The diagonal edge length of the body-centered cubic unit cell is $a\sqrt 3$. We will determine the radius of the atom present in BCC first then the distance (in${{\text{A}}^{\text{o}}}$) between nearest neighbours. In BCC two atoms touch each other.

Formula used: $r\, = \dfrac{{a\sqrt 3 }}{4}$

Complete step-by-step solution: The formula which is used to determine the atomic radius of a body-centered cubic unit cell is given as follows:
$r\, = \dfrac{{a\sqrt 3 }}{4}$
Where,
$r\,$is the atomic radius.
$a$ is the edge length of the unit cell.
Substitute ${\text{5}}{\text{.2}}\,{{\text{A}}^{\text{o}}}$ for the edge length of the unit cell.
$r\, = \dfrac{{{\text{5}}{\text{.2}}\,{{\text{A}}^{\text{o}}} \times \sqrt 3 }}{4}$
$r\, = 2.25\,{{\text{A}}^{\text{o}}}$
So, the atomic radius of the body-centered cubic unit cell of the potassium atom is$2.25\,{{\text{A}}^{\text{o}}}$.
The neighbour atoms in BCC are shown as follows:

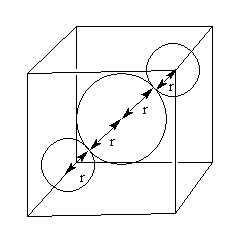
The distance between two neighbour atoms is $2$r so,
$= 2\, \times 2.25\,{{\text{A}}^{\text{o}}}$
$= 4.5\,{{\text{A}}^{\text{o}}}$
So, the distance (in${{\text{A}}^{\text{o}}}$) between nearest neighbours is $4.5\,{{\text{A}}^{\text{o}}}$.

Therefore, option (D) none of the above, is correct.

Additional information: Different types of unit cell have different edge length and radius. In face-centered cubic lattice, the diagonal edge length is $a\sqrt 2$ so, the radius is the one-fourth of the edge length $a\sqrt 2$ . The formula to determine the radius of face-centered cubic lattice is as follows:
$r\, = \dfrac{{a\sqrt 2 }}{4}$
In case of simple cubic unit cell, the edge length is taken as $a$ so, the formula which relates the edge length with atomic radius is ${\text{a}}\,{\text{ = }}\,{\text{2r}}$.

Note: The atomic radius is one-fourth of the edge length for the BCC unit cell. The edge length depends upon the type of unit cell, so the relationship between edge length and atomic radius also depends upon the type of unit cell. In the different unit cells, the arrangement of atoms is different. So, the edge length is different.