Question

Positive and negative point charges of equal magnitude are kept at $\left(0,0,\dfrac{a}{2}\right)$ and $\left(0,0,\dfrac{-a}{2}\right)$, respectively. The work done by the electric field when another positive point charge is moved from $(-a,0,0)$ to $(0,a,0)$ is:
A. positive
B. negative
C. Zero
D. depends on the path connecting the initial and the final positions

Answer 1

Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. We also know that the electric potential due to a charge is defined as the amount of energy needed to move a unit positive charge to infinity.
Formula:
$V=\dfrac{kq}{r}$

Complete step-by-step solution
We also know that the electric potential due to a charge $q$ is defined as the amount of energy needed to move a unit positive charge to infinity. Also the potential at any point is the vector sum of potentials at that point. Also, potential energy is defined as the work done in moving a unit positive charge from infinity.
Also, potential is proportional to the charge and inversely proportional to the distance between the point and the charge. $V = \dfrac{{kq}}{r}$, where $r$ is the distance between the unit charges and which is a constant.
Consider the point A $\left( {0,0,\dfrac{a}{2}} \right)$ and B $\left( {0,0,\dfrac{{ - a}}{2}} \right)$ in space. Such that $q$ and $- q$ are placed respectively. Consider another positive charge $Q$ to move from S $( - a,0,0)$ to T $(0,a,0)$as shown in figure below:

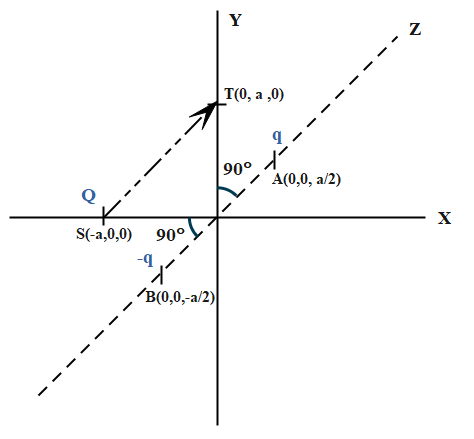
From the diagram it is clear that the two point charges q and –q form a dipole with distance 2a between them. Also, that angle between the three axes must be 90 degrees as they are mutually perpendicular to each other.
Now, the work done W, to move the charge Q from point S to T will be given by:
$W = q\left( {{V_B} - {V_A}} \right)$
But if we look at the dipole system alone, then the charge Q lies on its equatorial surface as shown in figure below:

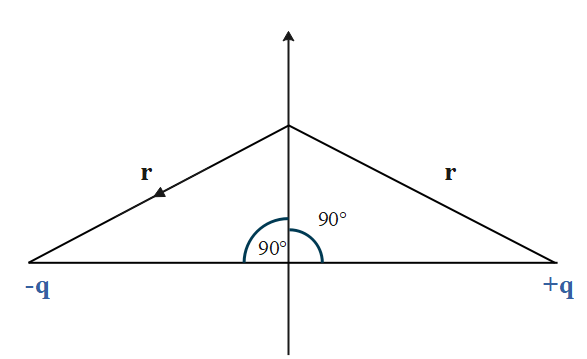
So if we find potential at a point having distance r from both the charges, we have:
\eqalign{ & V = {V_{ - q}} + {V_{ + q}} \cr & V = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\left( { - q + q} \right) = 0 \cr}
Hence clearly for the given system also, ${V_B} - {V_A} = 0$ as the axes are mutually perpendicular to each other. So the work done will be given as:
\eqalign{ & W = q\left( {{V_B} - {V_A}} \right) \cr & \Rightarrow W = q\left( 0 \right) \cr & \therefore W = 0 \cr}
Therefore, the correct option is C, i.e. the work done by the electric field when another positive point charge is moved from $( - a,0,0)$ to $(0,a,0)$ is zero.

Note: Since the charges are opposite to each other, we can say that AB acts as dipoles of some length along the z-axis. Now the point S and T are on the x and y-axis respectively. Since x, y, and z are perpendicular to each other, we can say that the new point is at the equatorial position with respect to the AB dipole. Hence the potential at S and T with respect to the dipole AB is always 0.