Solveeit Logo
Login

Question

Question: Position vector of a particle varies with time as $\overrightarrow{r} = t^2\hat{i} + t\hat{j} + 2\sq...

Position vector of a particle varies with time as r→=t2i^+tj^+2tk^\overrightarrow{r} = t^2\hat{i} + t\hat{j} + 2\sqrt{t}\hat{k}. Match the List-I with List-II.

List-IList-II
(P) From t= 0 to t = 1 magnitude of average velocity (In m/s)(1) 1265312\sqrt{\frac{6}{53}}
(Q) From t = 1 to t = 4 magnitude of average acceleration (In m/s²)(2) 1456\frac{\sqrt{145}}{6}
(R) At t = 1, rate of moving away from origin (In m/s)(3) 26532\sqrt{\frac{6}{53}}
(S) At t = 1, radius of curvature of path of the particle (In m)(4) 56\frac{5}{\sqrt{6}}
(5) 6\sqrt{6}

Choose the correct answer from the options given below.

Answer

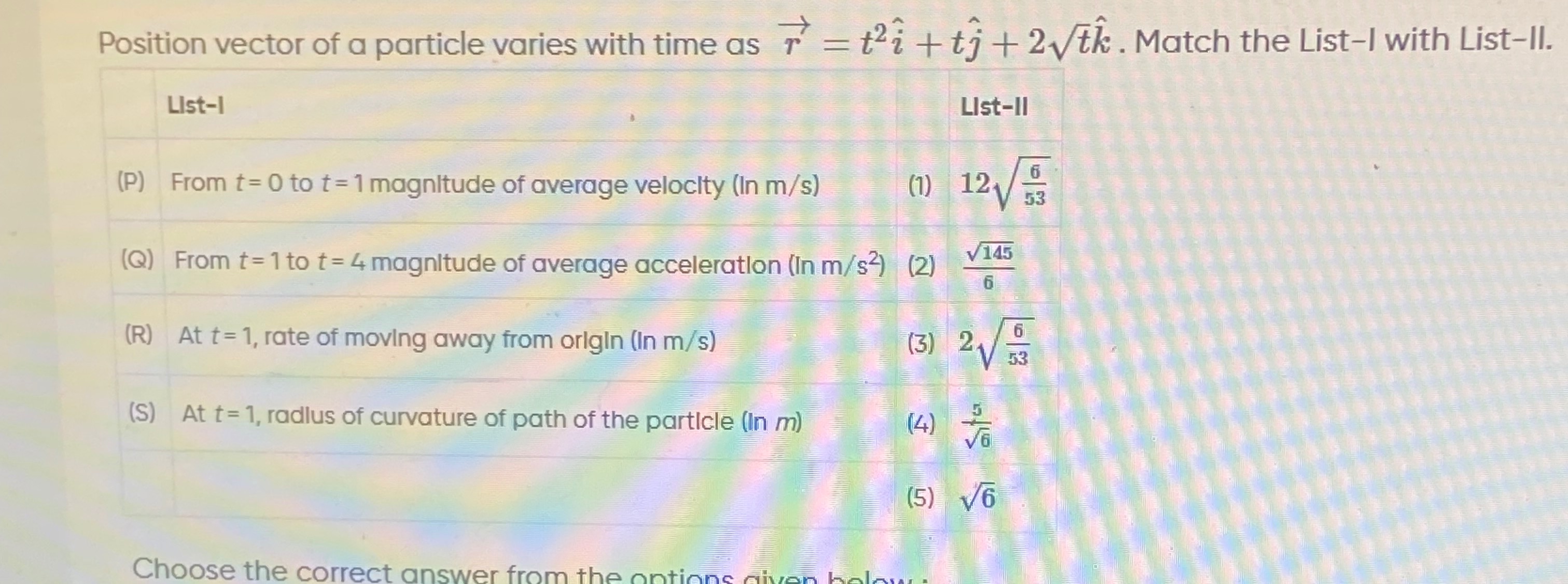
P: (5), Q: (2), R: (4), S: (1)

Explanation

Solution

Given:

r⃗(t)=t2 i^+t j^+2t k^\vec{r}(t)= t^2\,\hat{i} + t\,\hat{j} + 2\sqrt{t}\,\hat{k}
  1. (P) Average velocity from t=0t=0 to t=1t=1:

 r⃗(1)=(1,1,2)\vec{r}(1)=(1,1,2) and r⃗(0)=(0,0,0)\vec{r}(0)=(0,0,0).

 Displacement = (1,1,2)=\,(1,1,2) with magnitude

 $$ \sqrt{1^2+1^2+2^2}=\sqrt{6}.

 Time interval $=1$ s so average velocity magnitude $=\sqrt{6}$ which matches option **(5)**. 2. **(Q) Average acceleration from $ t=1 $ to $ t=4 $:**  First, find velocity:  $$ \vec{v}(t)=\frac{d\vec{r}}{dt}=\left(2t,\,1,\,\frac{1}{\sqrt{t}}\right).

 At t=1t=1: v⃗(1)=(2,1,1)\vec{v}(1)=(2,1,1).

 At t=4t=4: v⃗(4)=(8,1,1/2)\vec{v}(4)=(8,1,1/2).

 Difference: Δv⃗=(6,0,−12)\Delta \vec{v}=(6,0,-\frac{1}{2}).

 Magnitude of Δv⃗\Delta \vec{v}:

 $$ \sqrt{6^2+0^2+\left(\frac{1}{2}\right)^2}=\sqrt{36+\frac{1}{4}}=\sqrt{\frac{145}{4}}=\frac{\sqrt{145}}{2}.

 Time interval is $3$ s, so average acceleration magnitude:  $$ \frac{\sqrt{145}}{2\cdot 3}=\frac{\sqrt{145}}{6},

 which matches option (2).

  1. (R) Rate of moving away from the origin at t=1t=1:

 This rate is given by r⃗⋅v⃗∣r⃗∣\displaystyle \frac{\vec{r}\cdot\vec{v}}{|\vec{r}|}.

 At t=1t=1: r⃗=(1,1,2)\vec{r}=(1,1,2) and ∣r⃗∣=6 |\vec{r}|=\sqrt{6}; v⃗=(2,1,1)\vec{v}=(2,1,1).

 Dot product: 1⋅2+1⋅1+2⋅1=51\cdot2+1\cdot1+2\cdot1=5.

 Thus the rate =56=\frac{5}{\sqrt{6}} which equals option (4).

  1. (S) Radius of curvature at t=1t=1:

 Curvature κ=∣v⃗×a⃗∣∣v⃗∣3\kappa = \frac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3}, and radius of curvature ρ=1κ\rho=\frac{1}{\kappa}.

 Acceleration:  $$ \vec{a}(t)=\frac{d\vec{v}}{dt}=\left(2,,0,,-\frac{1}{2t^{3/2}}\right).

 At $ t=1 $: $\vec{a}(1)=(2,0,-\frac{1}{2})$ and $\vec{v}(1)=(2,1,1)$.  Compute $\vec{v}\times\vec{a}$:  $$ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 1 \\ 2 & 0 & -\frac{1}{2} \end{vmatrix} = -\frac{1}{2}\,\hat{i} + 3\,\hat{j} -2\,\hat{k}.

 Magnitude:

 $$ \sqrt{\left(-\frac{1}{2}\right)^2+3^2+(-2)^2}=\sqrt{\frac{1}{4}+9+4}=\frac{\sqrt{53}}{2}.

 Also, $ |\vec{v}(1)|=\sqrt{2^2+1^2+1^2}=\sqrt{6} $ so $ |\vec{v}(1)|^3=6\sqrt{6} $.  Thus, $\kappa=\frac{\sqrt{53}/2}{6\sqrt{6}}=\frac{\sqrt{53}}{12\sqrt{6}}$ and  $$ \rho=\frac{1}{\kappa}=\frac{12\sqrt{6}}{\sqrt{53}}=12\sqrt{\frac{6}{53}},

 which matches option (1).

Mapping:

  • P → (5)
  • Q → (2)
  • R → (4)
  • S → (1)