Solveeit Logo
Login

Question

Question: Position-time graph of a body of mass 5 kg is given in the diagram. The impulse on body at \(t=3s\) ...

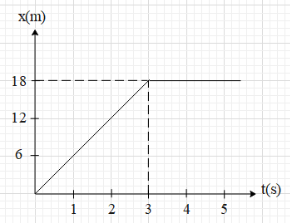
Position-time graph of a body of mass 5 kg is given in the diagram. The impulse on body at t=3st=3s is

A. 30i^kgms−130\widehat{i}kgm{{s}^{-1}}
B. −30i^kgms−1-30\widehat{i}kgm{{s}^{-1}}
C. 6i^kgms−16\widehat{i}kgm{{s}^{-1}}
D. −6i^kgms−1-6\widehat{i}kgm{{s}^{-1}}

Explanation

Solution

Analyse the given graph. Check what is happening to the motion of the body before time t=3st=3s and after time t=3st=3s and calculate the velocities before and after t=3st=3s. Then use the formula for impulse and calculate the impulse on the body at t=3st=3s.

Formula used:
v=ΔxΔtv=\dfrac{\Delta x}{\Delta t}
where v is the constant velocity of a body with change in position of Δx\Delta x in a time interval of Δt\Delta t.
ΔP=m(v2−v1)\Delta P=m\left( {{v}_{2}}-{{v}_{1}} \right)
where ΔP\Delta P is the impulse on a body of mass m when its velocity change from v2{{v}_{2}} to v1{{v}_{1}}.

Complete step by step answer:
For the given figure, we can see that the graph of position – time graph of the body shows a straight line before time t=3st=3s. This means that the position of the body is changing uniformly with respect to time. Therefore, the body is travelling with constant velocity before time t=3st=3s.With this, the speed of the body before t=3st=3s is v1=ΔxΔt{{v}_{1}}=\dfrac{\Delta x}{\Delta t} … (i)
From the graph, we get that Δx=18m\Delta x=18m and Δt=3s\Delta t=3s.
Substitute these values in equation (i).
⇒v1=183=6ms−1\Rightarrow {{v}_{1}}=\dfrac{18}{3}=6m{{s}^{-1}}
Now, in the graph we can see that just after time t=3st=3s the position of the body remains constant with respect to time. This means that the body comes to rest at time t=3st=3s, and remains at rest. Since the body is at rest, its velocity is zero i.e. v2=0{{v}_{2}}=0.

This means that at time t=3st=3s, the velocity of the body change from v1=6ms−1{{v}_{1}}=6m{{s}^{-1}} to v2=0{{v}_{2}}=0.
Therefore, the impulse on the body at t=3st=3s is ΔP=m(v2−v1)=5(0−6)=−30kgms−1\Delta P=m\left( {{v}_{2}}-{{v}_{1}} \right)=5\left( 0-6 \right)=-30kgm{{s}^{-1}}.
Now, since the body’s position is increasing along the x-axis, we can write the impulse in vector form as −30i^kgms−1-30\widehat{i}kgm{{s}^{-1}}.

Hence, the correct option is B.

Note: Some of the students may not know what is meant by impulse created on a body Impulse on a body is the change in momentum created in a body.Note that it is final momentum minus initial momentum. Some students may make a mistake by subtracting the initial momentum from the final momentum.