Question

Position of a particle is given by $y = \frac{t^2+t^3}{8}$. If % error in calculating time is 0.1% at t = 2 s, find % error in calculating position of the particle at t = 2 s.

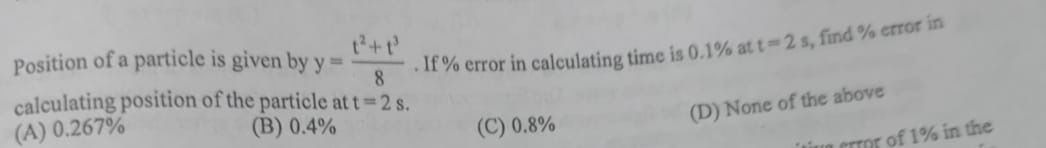
• A. 0.267%
• B. 0.4%
• C. 0.8%
• D. None of the above

Answer 1

Answer: (A)

0.267%

Answer 2

The position of the particle is given by the function: $y = \frac{t^2+t^3}{8}$

We are given that the percentage error in calculating time at $t = 2$ s is 0.1%. This can be written as: $\frac{\Delta t}{t} \times 100\% = 0.1\%$

To find the error in position $\Delta y$, we use the concept of error propagation. For a function $y = f(t)$, the change in $y$ for a small change in $t$ is given by $\Delta y \approx \frac{dy}{dt} \Delta t$.

We can also use relative errors: $\frac{\Delta y}{y} \approx \frac{dy}{dt} \frac{\Delta t}{y}$ Rearranging this, we get: $\frac{\Delta y}{y} \times 100\% \approx \left(\frac{dy}{dt} \frac{t}{y}\right) \left(\frac{\Delta t}{t} \times 100\%\right)$

First, let's find the value of $y$ at $t = 2$ s: $y(2) = \frac{(2)^2 + (2)^3}{8} = \frac{4 + 8}{8} = \frac{12}{8} = 1.5$

Next, we find the derivative of $y$ with respect to $t$: $\frac{dy}{dt} = \frac{d}{dt}\left(\frac{t^2+t^3}{8}\right) = \frac{1}{8}(2t + 3t^2)$

Now, we evaluate the derivative at $t = 2$ s: $\frac{dy}{dt}\Big|_{t=2} = \frac{1}{8}(2(2) + 3(2)^2) = \frac{1}{8}(4 + 3(4)) = \frac{1}{8}(4 + 12) = \frac{16}{8} = 2$

Now, substitute the values at $t=2$ s into the relative error formula: $\frac{\Delta y}{y} \times 100\% \approx \left(\frac{dy}{dt} \frac{t}{y}\right) \left(\frac{\Delta t}{t} \times 100\%\right)$ $\frac{\Delta y}{y} \times 100\% \approx \left(\frac{2 \times 2}{1.5}\right) \times 0.1\%$ $\frac{\Delta y}{y} \times 100\% \approx \left(\frac{4}{1.5}\right) \times 0.1\%$ $\frac{\Delta y}{y} \times 100\% \approx \left(\frac{40}{15}\right) \times 0.1\% = \frac{8}{3} \times 0.1\% = \frac{0.8}{3}\% \approx 0.2666... \%$

Rounding to three decimal places, the percentage error in position is approximately $0.267\%$.