Question
Question: Position of a particle is given by $\vec{r} = v_y\hat{i} + t^4\hat{j}$ (where t is time in second). ...
Position of a particle is given by r=vyi^+t4j^ (where t is time in second). Find magnitude of acceleration of the particle at t = 2 seconds. (vy represents velocity along y-axis)
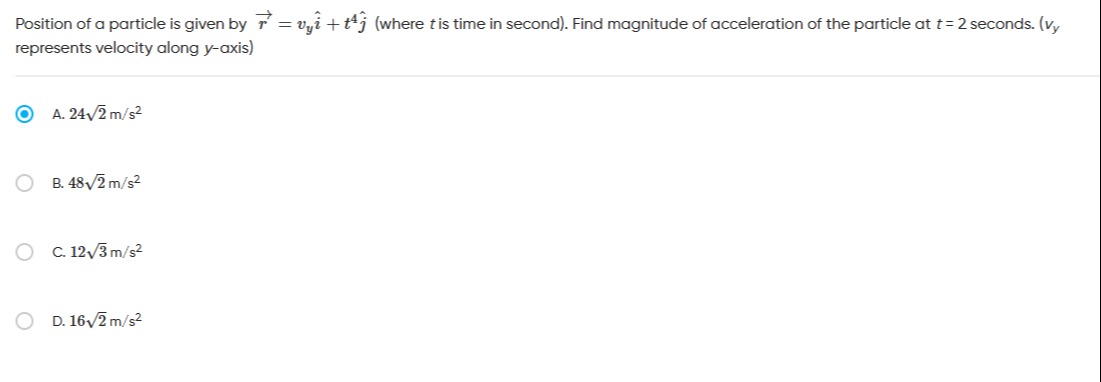
242 m/s²
482 m/s²
123 m/s²
162 m/s²
482 m/s²
Solution
The position vector of the particle is given by r=vyi^+t4j^. This implies that the components of the position vector are x(t)=vy and y(t)=t4. The problem states that "vy represents velocity along y-axis", meaning vy=dtdy. Given y(t)=t4, we find vy=dtdy=4t3. Therefore, the x-component of the position vector is x(t)=4t3. The position vector as a function of time is r(t)=4t3i^+t4j^. The velocity vector is obtained by differentiating the position vector with respect to time: v(t)=dtdr=dtd(4t3i^+t4j^)=12t2i^+4t3j^. The acceleration vector is obtained by differentiating the velocity vector with respect to time: a(t)=dtdv=dtd(12t2i^+4t3j^)=24ti^+12t2j^. At t=2 seconds, the acceleration vector is: a(2)=24(2)i^+12(22)j^=48i^+48j^ m/s². The magnitude of the acceleration is ∣a(2)∣=(48)2+(48)2=2×482=482 m/s².
