Question

Polarizing angle for water is ${{53}^{\circ }}{{4}^{'}}$. If light is incident at this angle on water and reflected the angle of refraction is
$\begin{aligned} & a){{126}^{\circ }}{{56}^{'}} \\\ & b){{36}^{\circ }}{{56}^{'}} \\\ & c){{30}^{\circ }} \\\ & d){{36}^{\circ }}{{20}^{'}} \\\ \end{aligned}$

Answer 1

When the light incident on to the surface of another medium undergoes polarization when the refracted ray and the reflected ray both are at an angle of 90 degrees. It is also to be noted that the reflected and the incident ray are at the same angle. Hence from this information we can easily write an equation describing the relation between the incident ray and the refracted ray and determine the refracted angle.

Complete step by step answer:
To begin with let us first understand what do you mean by polarized light.

Light basically is a wave consisting of electric and magnetic field components oscillating perpendicular to each other in the direction of propagation of the light wave. When light undergoes polarization, one of the components of light oscillating transverse in the direction of light is not carried further. In the above case the light gets polarized when incident on the surface of the and the polarized light gets reflected from the surface. Figure below is a pictorial representation of the above scenario.

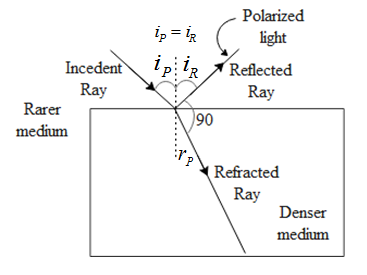
In the above figure the reflected ray makes an angle 90 degrees with the refracted ray. let us say the reflected ray makes an angle ${{i}_{R}}$ with respect to the normal of the surface of water and the refracted ray makes an angle ${{r}_{P}}$ with the normal of incidence. Hence we can say that,
${{i}_{R}}+{{r}_{P}}+90=180\text{ sum of the angle along a line is 180}$. Further we can write this as ${{i}_{R}}+{{r}_{P}}=90\text{ }$. Now since angle of incidence i.e. ${{i}_{P}}$ is equal to angle of reflection, let us replace the angle of reflection by the angle of incidence. After substituting we get,
${{i}_{P}}+{{r}_{P}}=90\text{ }....\text{(1)}$

The above angle of incidence is given in degrees and minutes. Let us entirely convert to degrees.
${{i}_{P}}={{53}^{\circ }}{{4}^{'}}$ the bar on the four represents minute. To convert it to degrees divide it by 60. Hence ${{4}^{'}}={{\left( \dfrac{1}{15} \right)}^{\circ }}$,hence the angle of incidence becomes ${{i}_{P}}={{53}^{\circ }}+{{\left( \dfrac{1}{15} \right)}^{\circ }}={{53.066}^{\circ }}$. Substituting the value of angle of incidence in equation 1 we get,

$53.066+{{r}_{P}}=90\text{ hence }{{r}_{P}}={{36.934}^{\circ }}$. But the options provided are again in terms of degrees and minute. Hence we now multiply 60 to 0.934 which is equal to 56.
Hence ${{r}_{P}}={{36}^{\circ }}{{56}^{'}}$ in terms of degree minutes.
Hence, the correct answer is option B.

Note:
The angle of incidence for which the reflected light will get polarized depends on the medium on which the light is incident on. To be more precise, it also depends both on the mediums the rarer as well as the denser. The effect of a polarized light is that the intensity of the light decreases.