Solveeit Logo
Login

Question

Question: Points \(A\left( 3,2,4 \right)\) , \(B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right)\) and...

Points A(3,2,4)A\left( 3,2,4 \right) , B(335,285,385)B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right) and C(9,8,10)C\left( 9,8,10 \right) are given. The ratio in which BB divides the segment ACAC is.
(a) 5:35:3
(b) 2:12:1
(c) 1:31:3
(d) 3:23:2

Explanation

Solution

Hint: For solving this question we will use the distance formula to find the length of segments between each point and check whether the given points are collinear or not. And if the points are collinear then we will solve for the correct answer.

Complete step-by-step answer:
Given:
Points A(3,2,4)A\left( 3,2,4 \right) , B(335,285,385)B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right) and C(9,8,10)C\left( 9,8,10 \right) are given.
Now, first, we will check whether the given points are collinear or not and we will do it by determining the direction ratio of the line through AB and direction ratio of the line through AC. And if both the direction ratios are proportional then the points will be collinear.
Direction ratio of a line passing through points P(x1,y1,z1)P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) and Q(x2,y2,z2)Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is equal to (x2−x1,y2−y1,z2−z1)\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right) .
Then, the direction ratio of line through AB =(185,185,185)=\left( \dfrac{18}{5},\dfrac{18}{5},\dfrac{18}{5} \right) .
Similarly, direction ratio of the line through AC =(6,6,6)=\left( 6,6,6 \right) .
Now, as both the direction ratios are proportional so, the points A(3,2,4)A\left( 3,2,4 \right) , B(335,285,385)B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right) and C(9,8,10)C\left( 9,8,10 \right) are collinear. For more clarity look at the figure given below:


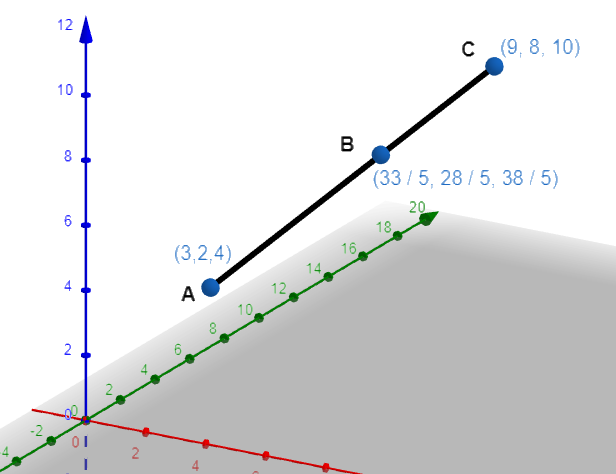
Now, we will use the distance formula written below:
Distance between points P(x1,y1,z1) and Q(x2,y2,z2)=(x2−x1)2+(y2−y1)2+(z2−z1)2P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\text{ and }Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}} .
Then, the distance between A(3,2,4)A\left( 3,2,4 \right) and C(9,8,10)C\left( 9,8,10 \right) =AC=62+62+62=63=AC=\sqrt{{{6}^{2}}+{{6}^{2}}+{{6}^{2}}}=6\sqrt{3} .
Similarly, between A(3,2,4) and B(335,285,385)=AB=(185)2+(185)2+(185)2=1835A\left( 3,2,4 \right)\text{ and }B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right)=AB=\sqrt{{{\left( \dfrac{18}{5} \right)}^{2}}+{{\left( \dfrac{18}{5} \right)}^{2}}+{{\left( \dfrac{18}{5} \right)}^{2}}}=\dfrac{18\sqrt{3}}{5} .
Similarly, between B(335,285,385) and C(9,8,10)=BC=(125)2+(125)2+(125)2=1235B\left( \dfrac{33}{5},\dfrac{28}{5},\dfrac{38}{5} \right)\text{ and }C\left( 9,8,10 \right)=BC=\sqrt{{{\left( \dfrac{12}{5} \right)}^{2}}+{{\left( \dfrac{12}{5} \right)}^{2}}+{{\left( \dfrac{12}{5} \right)}^{2}}}=\dfrac{12\sqrt{3}}{5} .
Now, as we know that points A, B and C are collinear, and it is evident from the length of AC, AB and BC that B will lie between A and C. Then, ABBC=1835×5123=32\dfrac{AB}{BC}=\dfrac{18\sqrt{3}}{5}\times \dfrac{5}{12\sqrt{3}}=\dfrac{3}{2} .
Thus, point B divides the segment AC in the ratio of 3:23:2 .
Hence, (d) is the correct option.

Note: Here, the student should first check whether the points are collinear though in this question the points are collinear and then apply distance formula correctly to get the correct answer. We can solve such a question with the help of a vector approach as well in which we will first find the position vector of point A and point C with respect to point B then ratio of the magnitudes of the vector will be the answer.