Question

Points A and B are in the first quadrant. Point $O$ is the origin. If the slope of ${OA}$ is $1$ , the slope of ${OB}$ is $7$ and $OA = OB$ then what is the slope of ${AB}$?
A). $- \dfrac{1}{5}$
B). $- \dfrac{1}{4}$
C). $- \dfrac{1}{3}$
D). $- \dfrac{1}{2}$

Answer 1

In this question, given that the points $A$ and $B$ are in the first quadrant. The point $O$ is the origin. And also given the slope of ${OA}$ and ${OB}$ are $1$ and $7$ respectively. Then here we need to find the slope of ${AB}$ . By using slope formula and distance formula we can find the slope of ${AB}$.

Formula used :
Slope, $m\ = \dfrac{\left(\text{Change in y} \right)}{\text{Change in x}}$
$m = (y{_2}- y{_1} ) /(x{_2} - x{_1})$
The formula for the distance between two points $(a,\ b)$ and $(c,\ d)$ is
$d = \sqrt{\left( c – a \right)^{2} + \left( d – b \right)^{2}}$

Complete step-by-step solution:

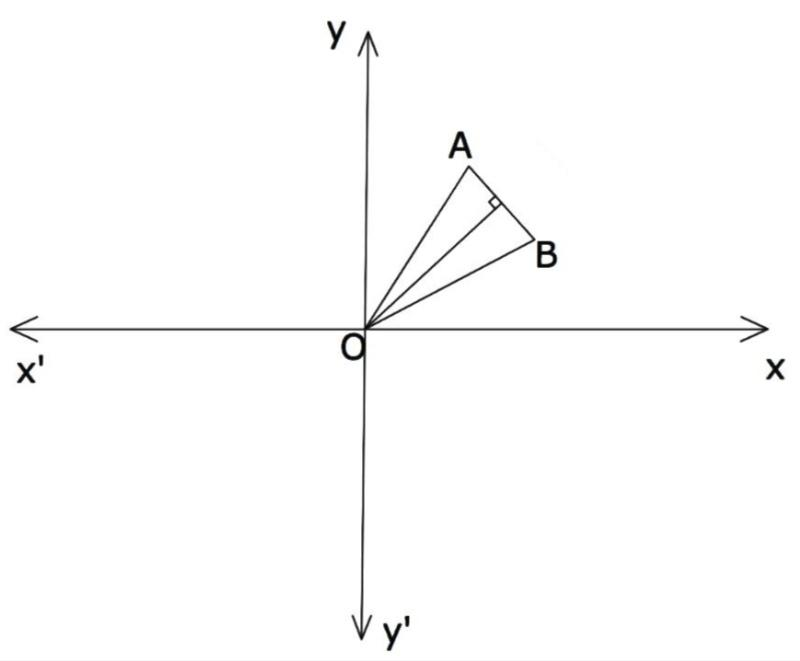
Let the point $A$ be $(a,\ b)$ and $B$ be $(c,\ d)$ be in the first quadrant. The point $O$ in the origin be $(0,\ 0)$
Given,
Slope, $OA\ = 1$
$\dfrac{\left( b – 0 \right)}{a – 0}\ = 1$
$\dfrac{b}{a} = 1$
By cross multiplying,
We get,
$b = a$
Slope , $OB = 7$
$\dfrac{\left( d – 0 \right)}{c – 0}\ = 7$
$\dfrac{d}{c} = 7$
By cross multiplying,
We get,
$d = 7c$
Also given that,
$OA = OB$
By using distance formula,
$\sqrt{\left( a – 0 \right)^{2} + \left( b – 0 \right)^{2}} = \sqrt{\left( c – 0 \right)^{2}\left( d – 0 \right)^{2}}$
On squaring both sides,
We get,
$a^{2} + b^{2} = c^{2} + d^{2}$
By substituting the values $b = a$an $d = 7c$
$a^{2} + a^{2} = c^{2} + \left( 7c \right)^{2}$
By removing the parentheses,
$a^{2} + a^{2} = c^{2} + 49c^{2}$
By adding,
We get,
$2a^{2} = 50c^{2}$
By simplifying,
We get,
$a^{2} = 25c^{2}$
By taking square root on both sides,
We get,
$a = \pm 5c$
Thus we get $a = 5c$or $a = - 5c$
Since A is in the first quadrant,
$a = 5c$
Now we can find the slope of AB
Slope,
$AB = \dfrac{\left( d – b \right)}{c – a}$
By substituting the known values,
We get,
$AB = \dfrac{7c – a}{c – a}\$Since$\ b = a$
By substituting the value of $a = 5c$
$AB = \dfrac{7c – 5c}{c – 5c}$
By simplifying,
We get,
$AB = \dfrac{2c}{- 4c}$
By dividing,
We get,
${slope\ }AB = - \dfrac{1}{2}$
Thus the slope of ${AB}$ is $- \dfrac{1}{2}$
The slope of ${AB}$ is $- \dfrac{1}{2}$

Note: The slope of a line is defined as the measure of its Steepness. It is calculated by dividing the change in $y$ coordinate by change in $x$ co-ordinate. Mathematically, slope is denoted by the letter $m$. Slope is positive when m is greater than $0$ and when m is less than $0$, slope is negative. If the slope is equal to $0$ that means it is a constant function.