Solveeit Logo
Login

Question

Question: Points A (5, 3), B (─2, 3) and D (5, ─4) are three vertices of a square ABCD. Plot these points on a...

Points A (5, 3), B (─2, 3) and D (5, ─4) are three vertices of a square ABCD. Plot these points on a graph paper and hence find the coordinate of the vertex C.

Explanation

Solution

First of all, we will plot the points A, B and D according to the coordinates given in the question. On plotting the points, we can deduce which of the given vertices are adjacent to vertex C and which of the given vertices is opposite to the vertex C. To find the vertex C, we will assume variables for its coordinates. The vertex C will be such that it is equidistant from points adjacent to the vertices adjacent to it and that distance will be equal to the other two adjacent vertices of the square.

Complete step-by-step answer:
First of all, we will plot the points A (5, 3), B (─2, 3) and D (5, ─4) on the graph.

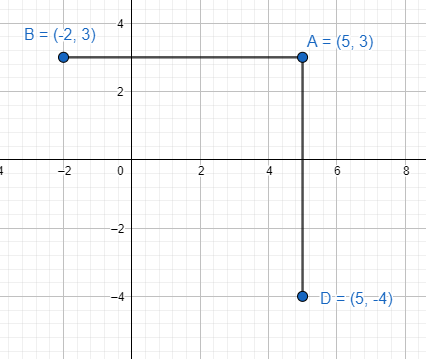
As we can see, point B and point D must be adjacent to point C to complete the square. Point A is opposite to point C.
We can find the length of a side of the square by finding the distance between vertex A and B. We will use the distance formula given as (x1−x2)2+(y1−y2)2\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}, where (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) are the points.
⇒dAB=(5+2)2+(3−3)2 ⇒dAB=7 \begin{aligned} & \Rightarrow {{d}_{AB}}=\sqrt{{{\left( 5+2 \right)}^{2}}+{{\left( 3-3 \right)}^{2}}} \\\ & \Rightarrow {{d}_{AB}}=7 \\\ \end{aligned}
Therefore, distance BC and CD must be 7, as the given figure is a square.
Let the coordinates of vertex C be (x, y).
Now, as we can see, the point C will be 7 units to the left of point D. We know the coordinates of point D are (5, ─4). So, we have to subtract 7 from the x – coordinate to go 7 units to the left.
Therefore, x = 5 – 7 = –2
Similarly, we need to go 7 units down from point B to find the y – coordinate of point C.
We know that the coordinates of point B are (–2, 3).
Therefore, y = 3 – 7 = –4
Thus, point C is (–2, –4).
Hence, the figure of the square is as follows:

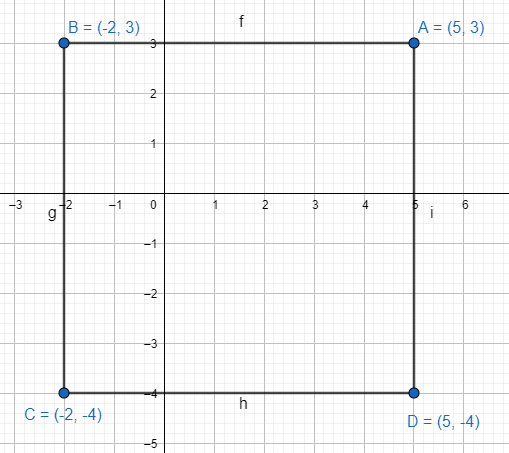
Note: We can also find vertex C as the mirror image of A about line BC. To find the mirror of A, we will find the point C, such that the midpoint of AC is coincident with the midpoint of BD and should lie on the equation of line perpendicular to BD and passing through point A.