Question

Point P(x, y) satisfying the equation ${{\sin }^{-1}}x+{{\cos }^{-1}}y+{{\cos }^{-1}}(2xy)=\pi /2$ lies on

1. The bisector of the first and third quadrant.
2. The bisector of the second and fourth quadrant.
   3)The rectangle formed by the lines x=$\pm$1 and y=$\pm$1
   4)A unit circle with centre at the origin

Answer 1

Convert the ${{\cos }^{-1}}y$ into the sine form and then use the formula ${{\sin }^{-1}}+{{\cos }^{-1}}x=\pi /2$
Simplify all the options given in the question
(1)The bisector of the first and third quadrant.
The line is bisecting and passing through first and third quadrant
$\Rightarrow$ x=y

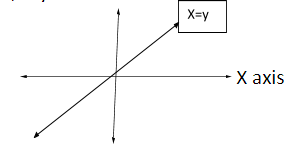
(2)The bisector of the second and fourth quadrant.
The line is bisecting and passing through second and fourth quadrant
$\Rightarrow$x=-y

      ![](https://www.vedantu.com/question-sets/b1d7c41e-862f-4dd6-bc1e-17eea5b2c9894979509385373628855.png)  

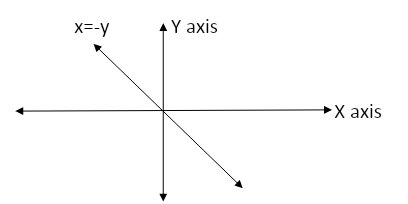
(3)The rectangle formed by the lines x=$\pm$1 and y=$\pm$1

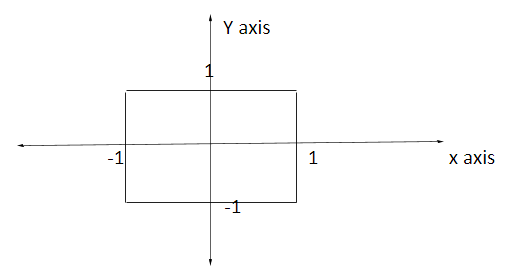
(4) A unit circle with centre at the origin

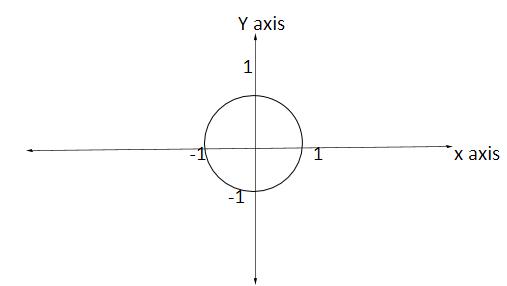
The equation for this circle is ${{x}^{2}}+{{y}^{2}}=1$

Formula Used:
$\begin{aligned} & \cos \theta =Base/Hypotenuse \\\ & \sin \theta =Perpendicular/Hypotenuse \\\ & {{\sin }^{-1}}x+{{\sin }^{-1}}y={{\sin }^{-1}}[xy+\sqrt{1-y}\sqrt{1-{{x}^{2}}}] \\\ \end{aligned}$
${{\sin }^{-1}}x+{{\cos }^{-1}}x=\pi /2$

Complete step-by-step answer:
${{\sin }^{-1}}x+{{\cos }^{-1}}y+{{\cos }^{-1}}(2xy)=\pi /2$ (1)
Convert the ${{\cos }^{-1}}y$ into the sine form

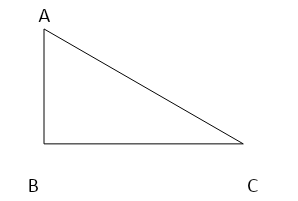
That is,
Let ${{\cos }^{-1}}y$ = $\theta$ in triangle ABC
{ $\angle ACB=\theta$}
$\Rightarrow$ cos $\theta$=y = Base/Hypotenuse
$\Rightarrow$Base=y
$\Rightarrow$Hypotenuse=1
Applying the Pythagoras theorem
Hypotenuse$^{2}$ =Base$^{2}$ + Perpendicular$^{2}$
$\Rightarrow$1$^{2}$ = y$^{2}$ + Perpendicular$^{2}$
$\Rightarrow$ Perpendicular$^{2}$ =1$^{2}$ - y$^{2}$
Taking square root on both sides
We get,
Perpendicular = $\sqrt{1-{{y}^{2}}}$
$\Rightarrow$sin$\theta$= Perpendicular/Hypotenuse
= $\sqrt{1-{{y}^{2}}}$
Now,
Put the value of ${{\cos }^{-1}}y$ in terms of sine in equation (1)
$\begin{aligned} & {{\sin }^{-1}}x+{{\sin }^{-1}}\sqrt{1-{{y}^{2}}}+{{\cos }^{-1}}2xy=\pi /2 \\\ & \\\ \end{aligned}$ (2)
Use the formula ${{\sin }^{-1}}x+{{\sin }^{-1}}y={{\sin }^{-1}}[xy+\sqrt{1-y}\sqrt{1-{{x}^{2}}}]$
Here y= $\sqrt{1-{{y}^{2}}}$
$\Rightarrow$ ${{\sin }^{-1}}x+{{\sin }^{-1}}\sqrt{1-{{y}^{2}}}={{\sin }^{-1}}[x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}}]$
Put in equation (2)
${{\sin }^{-1}}[x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}}]+{{\cos }^{-1}}2xy=\pi /2$
Now,
We know that ${{\sin }^{-1}}x+{{\cos }^{-1}}x=\pi /2$
$\Rightarrow$$$x\sqrt{1-{{y}^{2}}}+y\sqrt{1-{{x}^{2}}}=2xy$$

& \Rightarrow \sqrt{1-{{y}^{2}}}\sqrt{1-{{x}^{2}}}=2xy-xy \\\ & \Rightarrow \sqrt{1-{{y}^{2}}}\sqrt{1-{{x}^{2}}}=xy \\\ \end{aligned}$$ Squaring on both sides We get $$\begin{aligned} & (1-{{y}^{2}})(1-{{x}^{2}})={{x}^{2}}{{y}^{2}} \\\ & \Rightarrow 1-{{y}^{2}}-{{x}^{2}}+{{x}^{2}}{{y}^{2}}={{x}^{2}}{{y}^{2}} \\\ & \Rightarrow 1-{{y}^{2}}-{{x}^{2}}={{x}^{2}}{{y}^{2}}-{{x}^{2}}{{y}^{2}} \\\ & \Rightarrow 1-{{y}^{2}}-{{x}^{2}}=0 \\\ & \Rightarrow {{y}^{2}}+{{x}^{2}}=1 \\\ \end{aligned}$$ Hence the right option is (4) that is A unit circle with centre at the origin. **Additional information:** The inverse trigonometric functions are also known as the anti trigonometric functions or sometimes called arcus functions or cyclometric functions. The formula list is given below for reference to solve the problems. $$\begin{aligned} & si{{n}^{-1}}x\text{ }+\text{ }co{{s}^{-1}}x\text{ }=\text{ }\pi /2\text{ },\text{ }x\in \left[ -1,\text{ }1 \right] \\\ & ta{{n}^{-1}}x\text{ }+\text{ }co{{t}^{-1}}x\text{ }=\text{ }\pi /2\text{ },\text{ }x\in R \\\ & se{{c}^{-1}}x\text{ }+\text{ }cose{{c}^{-1}}x\text{ }=\text{ }\pi /2\text{ },\left| x \right|\text{ }\ge \text{ }1 \\\ \end{aligned}$$ **Note:** The knowledge about the trigonometric functions as well as inverse trigonometric functions and their relations is important for students to answer such questions.