Question

Point $P$ is the point with the greatest $y-$ coordinate on the semicircle shown above. What is the $x-$ coordinate of point $Q$?

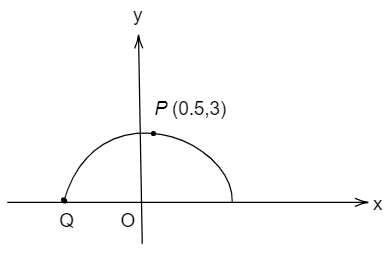
A. $-3.5$
B. $-3$
C. $-2.5$
D. $-2$
E. $-1.5$

Answer 1

Here we have been given two points in a semicircle. We know the coordinate of one point and by using it we have to find the coordinate of another point. Firstly as it is given that the point whose coordinate is given has the greatest $y-$ coordinate on the semi circle which means we can get the radius and the center of the semicircle by it. Then we will use this information and get the $x-$ coordinate of the other point.

Complete answer: The diagram is given as follows:

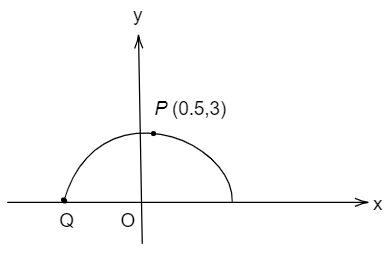
We can get the following information from the graph above,
$P=\left( 0.5,3 \right)$
The above point has the greatest $y-$ coordinate which means we can get the center and the radius of the semi circle by it as follows,
So center of the semicircle will be $\left( 0.5,0 \right)$
The Radius of the semicircle will be $3$ which is the $y-$ coordinate value as it is the highest value a semicircle can have.
As point $Q$ lies in the semicircle its distance from the center which is at $\left( 0.5,0 \right)$ will be equal to the radius of the semicircle which is $3$ .
So the $x-$ coordinate of the semicircle will be as follows:
$Q$ $x-$ Coordinate$=0.5-3$
$Q$ $x-$ Coordinate$=-2.5$
Hence the correct option is (C).

Note:
A semi-circle is often known as a half circle; it is formed when a line passing through the center of a circle touches the two ends of the circle. It has a full arc which measures to ${{180}^{\circ }}$ . It is very useful in constructing the arithmetic and geometric means of two lengths by the help of a straight-edge and compass. Area of the semicircle is always half the area of the circle it is formed from.