Question

Point $P$ is in the middle of the rectangle. What’s the electric field strength in $P$?

Here ${Q_1} = + 20.0\mu C$, ${Q_2} = - 40.0\mu C$, ${Q_3} = + 20.0\mu C$ and ${Q_4} = - 40.0\mu C$.

Answer 1

First draw a separate diagram showing the electric field strength for positive charges and negative charges respectively. We have to use the electric field strength formula to solve this problem, taking two cases. First find an electric field due to two positive charges then in second electric field strength due to two negative charges. Then add both the cases to get the total electric field strength in P.

Complete step by step answer:
As per the problem we have a figure having Point P is in the middle of the rectangle.Now we have to calculate the field at point P that is due to each charge separately. Since the four changes as give in the problem are points charges, the equation for the filed due to each individual change can be calculated using,
$E = \dfrac{{kQ}}{{{r^2}}}$
Where, electric field strength due to the charge is E and $k$ is a constant term which is equal to $9 \times {10^9}N{m^2}{C^{ - 2}}$.

The distance between the charges and the given point is $r$. Since P is at the center of the rectangle which is $20.0cm$ long and $10.0cm$ high. The distance r is equal in all the cases.

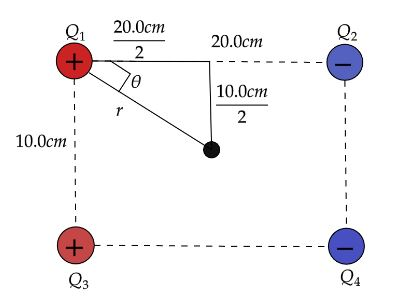
Hence the value of r using Pythagoras’s theorem,
$r = \sqrt {{{\left( {\dfrac{L}{2}} \right)}^2} + {{\left( {\dfrac{B}{2}} \right)}^2}}$
Where, $L$ is the length of the rectangle and $B$ is the height of the rectangle.
Now putting the values we will get the value of r as,
$r = \sqrt {{{\left( {\dfrac{{20.0cm}}{2}} \right)}^2} + {{\left( {\dfrac{{10.0}}{2}} \right)}^2}} = \sqrt {{{\left( {0.10m} \right)}^2} + {{\left( {0.05m} \right)}^2}}$

We can say ${r^2} = 0.0125{m^2}$
Q is the change.
The angle as represented in the figure is equal to,
$\tan \theta = \dfrac{5}{{10}}$
We can say,
$\theta = {\tan ^{ - 1}}\left( {\dfrac{5}{{10}}} \right) = 26.6^\circ$
Taking two different case one for the positive charges and the other for the negative charges we will get,

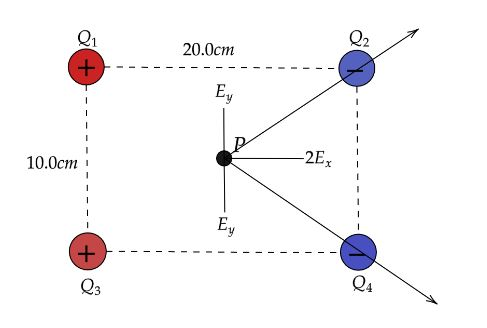
Case I: Since ${Q_1}\,{\text{and}}\,{Q_3}$ are equal we can find the electric field strength as,

${E_1} = {E_3} = \dfrac{{kQ}}{{{r^2}}}$
$\Rightarrow {Q_1} = + 20.0\mu C$
$\Rightarrow {Q_3} = + 20.0\mu C$
As we can see from the diagram that the y-component of the get cancels out and the x-component gets added up.Now the electric field due to one charge along the x-component is,
${E_1} = {E_X} = E\cos \theta$

Now, ${E_1} = \dfrac{{k{Q_1}\cos \theta }}{{{r^2}}}$
Putting all the known values we will get,
${E_1} = \dfrac{{9 \times {{10}^9} \times 20 \times {{10}^{ - 6}}\cos 26.6^\circ }}{{0.0125}} \Rightarrow {E_1}= 1.29 \times {10^7}N{C^{ - 1}}$
We know,
${E_1} = {E_3} = 1.29 \times {10^7}N{C^{ - 1}}$

Case II: Since ${Q_2}\,{\text{and}}\,{Q_4}$ are equal we can find the electric field strength as,

${E_2} = {E_4} = \dfrac{{kQ}}{{{r^2}}}$
$\Rightarrow {Q_2} = - 40.0\mu C$
$\Rightarrow {Q_4} = - 40.0\mu C$
As we can see from the diagram that the y-component of the get cancels out and the x-component gets added up.Now the electric field due to one charge along the x-component is,
${E_2} = {E_X} = E\cos \theta$

Now, ${E_2} = \dfrac{{k{Q_2}\cos \theta }}{{{r^2}}}$
Putting all the known values we will get,
${E_2} = \dfrac{{9 \times {{10}^9} \times 40 \times {{10}^{ - 6}}\cos 26.6^\circ }}{{0.0125}} = 2.58 \times {10^7}N{C^{ - 1}}$
We know,
${E_2} = {E_4} = 2.58 \times {10^7}N{C^{ - 1}}$
Thus the overall field at point P is,
${E_{total}} = {E_1} + {E_2} + {E_3} + {E_4}$
Putting the values we will get,
${E_{total}} = 1.29 \times {10^7}N{C^{ - 1}} + 1.29 \times {10^7}N{C^{ - 1}} + 2.58 \times {10^7}N{C^{ - 1}} + 2.58 \times {10^7}N{C^{ - 1}}$
$\therefore {E_{total}} = 7.74 \times {10^7}N{C^{ - 1}}$ in the positive x-direction.

Hence,the electric field strength in $P$ is $7.74 \times {10^7}N{C^{ - 1}}$.

Note: Electric field strength due to positive charge is along the outward direction while for the negative charge it is in inward direction. Remember that equal charges placed at equal distance from the given point produces equal electric strength. In the above solution the y-components are cancelled out because they are equal in magnitude but opposite in direction.