Question
Question: Point \(P\) and \(D\) are taken on the ellipse \({{\left( x+y-1 \right)}^{2}}+2{{\left( x+y-2 \right...
Point P and D are taken on the ellipse (x+y−1)2+2(x+y−2)2=8. If a,b,c,d are lengths of the quadrilateral PADB where A and B are foci of the ellipse. Then minimum value of a2+b2+c2+d2$$$$
A. 12B.16
C. 30$$$$
D. None of these
Solution
Draw the diagram of the ellipse and the quadrilateral. Replace the linear expressions in the equation of ellipse with new variables. Then use the fact that the sum of distances from a point to the foci is twice semi-major axis. Finally, use the inequality between arithmetic mean and geometric mean to find the required.
Complete step-by-step answer:
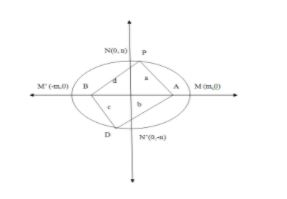
We have drawn the figure of the ellipse which cuts the coordinate axes at M(m,0),M′(−m,0),N(0,n),N′(0,−n). The segment MM′ is the major axis and NN′ is the minor axis. The length of semi-major axis is the distance of either M or M′ from the origin that is m
As given in the question P and D are any two points on the ellipse. The foci of the ellipse on the major axis are named as A and B. The quadrilateral formed by joining the four points is PADB . We denote the lengths of the sides as PA=a,AD=b,DB=c,PB=d.
The given equation of ellipse is
(x+y−1)2+2(x+y−2)2=8...(1)
Let us substitute x+y−1=X and x+y−2=Yas variables. We are replacing the combination variable with a single variable which will not change the shape of the ellipse. We know from the standard equation of ellipse with major-axis length 2m and minor axis length 2n that
m2x2+n2y2=1
We divide both side of equation (1) by 8 to convert it into above from,
8X2+4Y2=1
We also know from the property of ellipse that the sum of distances from to the two foci is constant and its value is 2m=2(22)=42.
Now P is a point on the ellipse whose sum of distances from the foci A and B is PA+PB=a+d=42 . Similarly the D is also a point on the ellipse whose sum of distances from the foci A and B is DA+DB=b+c=42. So
a+b+c+d=82
We use the inequality between arithmetic mean and geometric mean. Now,
