Question

Point 'O' is the centre of the ellipse with major axis AB & minor axis CD. Point F is one focus of the ellipse. If OF = 6 & the diameter of the inscribed circle of triangle OCF is 2, then find (AB) (CD).

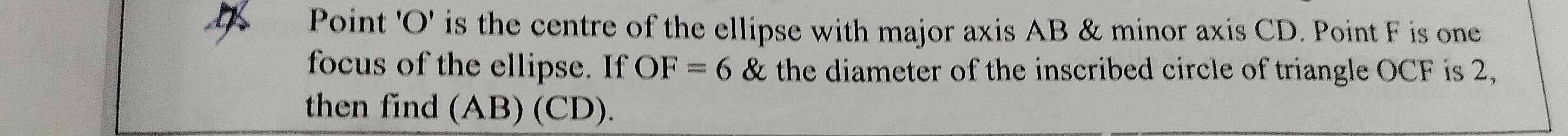
• A. 65
• B. 130
• C. 30
• D. 60

Answer 1

Answer: (A)

65

Answer 2

Let 'a' be the semi-major axis and 'b' be the semi-minor axis. The lengths of the major and minor axes are AB = 2a and CD = 2b, respectively. The distance from the center to a focus is 'c'. We are given OF = c = 6. Triangle OCF is a right-angled triangle with legs OC = b and OF = c = 6, and hypotenuse CF = $\sqrt{b^2 + c^2} = \sqrt{b^2 + 36}$. The inradius 'r' of a right-angled triangle is given by $r = \frac{\text{sum of legs} - \text{hypotenuse}}{2}$. We are given that the diameter of the inscribed circle is 2, so the inradius r = 1. Thus, $1 = \frac{b + 6 - \sqrt{b^2 + 36}}{2}$. Multiplying by 2, we get $2 = b + 6 - \sqrt{b^2 + 36}$. Rearranging, $\sqrt{b^2 + 36} = b + 4$. Squaring both sides: $b^2 + 36 = (b + 4)^2 = b^2 + 8b + 16$. This simplifies to $36 = 8b + 16$, so $8b = 20$, which gives $b = \frac{20}{8} = \frac{5}{2}$. For an ellipse, the relation between a, b, and c is $c^2 = a^2 - b^2$. Substituting the values: $6^2 = a^2 - (\frac{5}{2})^2$. $36 = a^2 - \frac{25}{4}$. $a^2 = 36 + \frac{25}{4} = \frac{144 + 25}{4} = \frac{169}{4}$. So, $a = \sqrt{\frac{169}{4}} = \frac{13}{2}$. We need to find (AB)(CD) = (2a)(2b) = 4ab. (AB)(CD) = $4 \times \frac{13}{2} \times \frac{5}{2} = 4 \times \frac{65}{4} = 65$.