Question

Point O is the centre of both circles in the figure above. If the circumference of the large circle is 36 and the radius of the small circle is half the radius of the large circle, what is the length of the smaller arc of the smaller circle?

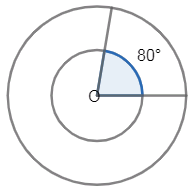
(a) 10
(b) 8
(c) 6
(d) 4

Answer 1

Hint:In this question, we first need to find the radius of the larger circle from the circumference formula and then on dividing it with 2 we get the radius of the smaller circle. Now, convert the given angle into radians and substitute the values of radius and use the formula of length of an arc i.e $l=r\theta$ to get the required answer.

Complete step-by-step answer:
Let us assume the radius of the larger circle as R and radius of the smaller circle as r.
As we already know the formula for the circumference of a circle
$2\pi R$
Now, on considering the circumference of the larger circle and substituting the respective values in the above formula we get,
$\Rightarrow 2\pi R=36$
Let us now divide with 2 on both the sides,
$\Rightarrow \pi R=18$
Now, on rearranging the terms on both the sides we get,
$\Rightarrow R=\dfrac{18}{\pi }$
As given in the question that radius of smaller circle is half the radius of the larger circle we get,
$\Rightarrow r=\dfrac{R}{2}$
$\Rightarrow r=\dfrac{18}{2\times \pi }$
$\Rightarrow r=\dfrac{9}{\pi }$
Now, let us convert the given angle in degrees to radians.
Let us assume the angle in radians as $\theta$
$\Rightarrow \theta =\dfrac{\pi }{180}\times d$
Given in the question that,
$d={{80}^{\circ }}$
Now, on substituting this value in the above formula we get,
$\Rightarrow \theta =\dfrac{\pi }{180}\times 80$
Now, on cancelling the common terms and simplifying it further we get,
$\Rightarrow \theta =\dfrac{4\pi }{9}$
As we already know that the length of an arc is given by the formula
$l=r\theta$
Now, by substituting the values of radius of the smaller circle and the angle made at the centre in the length of the arc formula we get,
$\Rightarrow l=r\theta$
Now, on substituting the respective values we get,
$\Rightarrow l=\dfrac{9}{\pi }\times \dfrac{4\pi }{9}$
Now, on cancelling the common terms and simplifying it further we get,
$\therefore l=4$
Hence, the correct option is (d).

Note: Instead of finding the value of the radius of the larger circle we can directly get the value of the smaller circle by substituting the value of radius of larger circle in terms of radius of smaller circle in the circumference formula. Both the methods give the same result.
It is important to note that while substituting the values corresponding values should be considered because considering the relation of the radii in the other way or substituting wrong values changes the result completely.Students should remember the formula of length of an arc i.e $l=r\theta$ .And also conversion of degree into radian or radian into degree.For conversion of degree into radian we have to multiply the degree by $\dfrac{\pi}{180}$ and for conversion of radian into degree we have to multiply radian by $\dfrac{180}{\pi}$.