Question

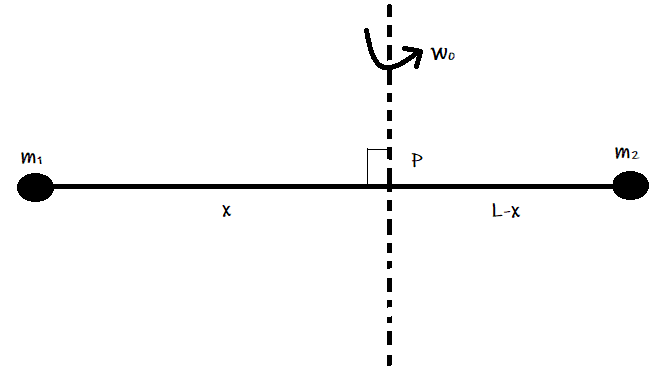
Point masses ${m_1}$ and ${m_2}$ are placed at the opposite ends of a rigid rod of length $L$ , and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ${\omega _0}$ is minimum, is given by:

(A) $x = \dfrac{{{m_2}L}}{{{m_1} + {m_2}}}$
(B) $x = \dfrac{{{m_1}L}}{{{m_1} + {m_2}}}$
(C) $x = \dfrac{{{m_1}}}{{{m_2}}}L$
(D) $x = \dfrac{{{m_2}}}{{{m_1}}}L$

Answer 1

Hint : Moment of inertia about both the point masses about the axis. Minimum work done is calculated by differentiating work with respect to $x$ and equating the result to zero.

Complete step by step answer
Moment of inertia is the name given to rotational inertia, the rotational analogue of mass for linear motion. It appears in the relationships for the dynamics of rotational motion. The moment of inertia must be specified with respect to a chosen axis of rotation. For a point mass the moment of inertia is just the mass times the square of perpendicular distance to the rotation axis, $I = m{r^2}$ .
Moment of inertia of point mass ${m_1}$ about the axis: ${I_1} = {m_1}{x^2}$ .
Moment of inertia of point mass ${m_2}$ about the axis: ${I_2} = {m_2}{\left( {L - x} \right)^2}$
Moment of inertia of the system about the axis of rotation (through point P) is $W = \dfrac{1}{2}I{\omega _0}^2 = \dfrac{1}{2}\left[ {{m_1}{x^2} + {m_2}{{\left( {L - x} \right)}^2}} \right]{\omega _0}^2$ .
As it is evident, the motion of the body is rotational. The energy possessed by the body is rotational kinetic energy.
Total work done is given by, $W = \dfrac{1}{2}{I_1}{\omega _0}^2 + \dfrac{1}{2}{I_2}{\omega _0}^2 = \dfrac{1}{2}{\omega _0}^2\left( {{m_1}{x^2} + {m_2}{{\left( {L - x} \right)}^2}} \right)$
By work energy theorem, work done to set the rod rotating with angular velocity ${\omega _0}$ is equal to the increase in rotational kinetic energy. Work done is a change in kinetic energy.
To minimize $W$ , we need to differentiate it with respect to $x$ and equate to zero.
$\dfrac{{dW}}{{dx}} = 0$
Thus, on differentiating $W = \dfrac{1}{2}{\omega _0}^2\left( {{m_1}{x^2} + {m_2}{{\left( {L - x} \right)}^2}} \right)$ ,
${m_1}x - {m_2}\left( {L - x} \right) = 0$
$\Rightarrow x = \dfrac{{{m_2}L}}{{{m_1} + {m_2}}}$
So the correct answer is option A.

Note
The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass as the central axis has mass evenly distributed around it thereby providing minimum resistance to rotation as compared to any other axis.
Thus, work done is minimum when the axis passes through the centre of mass.
Centre of mass is at $\dfrac{{{m_2}L}}{{{m_1} + {m_2}}}$ .
This is the position of centre of mass of the rod from ${m_1}$ . Hence the required axis should pass through the centre of mass of the rod and perpendicular to the length of the rod as shown in the figure.