Question

Point charges $+4q,+2q,+8q$ are placed at the corners B, A and C respectively of a square of side $0.2\;m$. Calculate the work done in moving the charge $+2q$ from the corner D to the centre of the square.

Answer 1

Electric field is the electric force due to a unit positive charge which is at rest exerted on its surrounding. We also know that the electric potential due to a charge is defined as the amount of energy needed to move a unit positive charge to infinity.

Formula: $V=\dfrac{kq}{r}$

Complete answer:
We also know that the electric potential due to a charge $q$ is defined as the amount of energy needed to move a unit positive charge to infinity. Also the potential at any point is the vector sum of potentials at that point. Also, potential energy is defined as the work done in moving a unit positive charge from infinity.
Also, potential is proportional to the charge and inversely proportional to the distance between the point and the charge. $V=\dfrac{kq}{r}$, where $r$ is the distance between the unit charges and $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is a constant.
Let us consider the diagram as shown below,

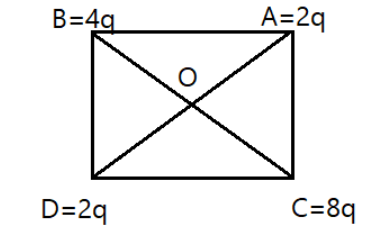
Given that $AB=BC=CD=DA=0.2m$
Then the diagonals $AC=BD=\sqrt(0.2)^{2}+(0.2)^{2}$
$\implies AC=BD=0.28m$
$\implies OA=OB=OC=OD=0.14m$
To find the work done in moving the charge from D to O, we must find the individual potential at D and O.
Then the potential energy at D is given as $V_{D}=\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{q_{A}}{AD}+\dfrac{q_{B}}{BD}+\dfrac{q_{C}}{CD}\right]$
$\implies V_{D}=\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{2q}{0.28}+\dfrac{4q}{0.2}+\dfrac{8q}{0.2}\right]$
Similarly, the potential energy at O is given as
$V_{O}=\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{q_{A}}{AO}+\dfrac{q_{B}}{BO}+\dfrac{q_{C}}{CO}\right]$
$\implies V_{O}=\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{2q}{0.14}+\dfrac{4q}{0.14}+\dfrac{8q}{0.14}\right]$
Then the work done $W$ is given as $W=q_{D}[V_{O}-V_{D}]$
On substitution, we get,
$W=2q\times \left(\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{2q}{0.14}+\dfrac{4q}{0.14}+\dfrac{8q}{0.14}\right]-\dfrac{1}{4\pi\epsilon_{0}}\left[\dfrac{2q}{0.28}+\dfrac{4q}{0.2}+\dfrac{8q}{0.2}\right]\right)$
$\implies W=\dfrac{2q}{4\pi\epsilon_{0}}\left[\dfrac{2q}{0.14}+\dfrac{4q}{0.14}+\dfrac{8q}{0.14}-\dfrac{2q}{0.28}-\dfrac{4q}{0.2}-\dfrac{8q}{0.2}\right]$
$\implies W=2q^{2}\times 9\times 10^{9}\left[\dfrac{14}{0.14}-\dfrac{1}{0.14}-\dfrac{12}{0.2}\right]$
$\implies W=2q^{2}\times 9\times 10^{9}\left[\dfrac{13}{0.14}-\dfrac{8.4}{0.14}\right]$
$\implies W=2q^{2}\times 9\times 10^{9}\left[\dfrac{4.6}{0.14}\right]$
$\implies W=18q^{2}\times 10^{9}\left[\dfrac{2.3}{0.07}\right]$
$\implies W=591.4q^{2}\times 10^{9}J$
$\therefore W=5.914q^{2}\times 10^{7}J$
Thus the total work done by the charge in moving from D to O is $5.91q^{2}\times 10^{7}J$

Note:
Potential energy is the energy of charge due to some position. Also, note that, $E=\dfrac{V}{r}$ where $r$ is the distance of the charge from the unit charge. Here, the change in potential energy is found which also the work is done by the charge.