Question

PNP’ is the double ordinate of the parabola. Prove that the locus of the point of intersection of the normal at $P$ and the diameter through ${{P}^{'}}$ is equal to the parabola ${{y}^{2}}=4a\left( x-4a \right)$.

Answer 1

Hint: The equation of diameter is given as $y=\dfrac{2a}{m}$ , where $m$ is the slope of the diameter.

A double ordinate is a chord which is perpendicular to the axis of the parabola .
Let the equation of the parabola be ${{y}^{2}}=4ax$.

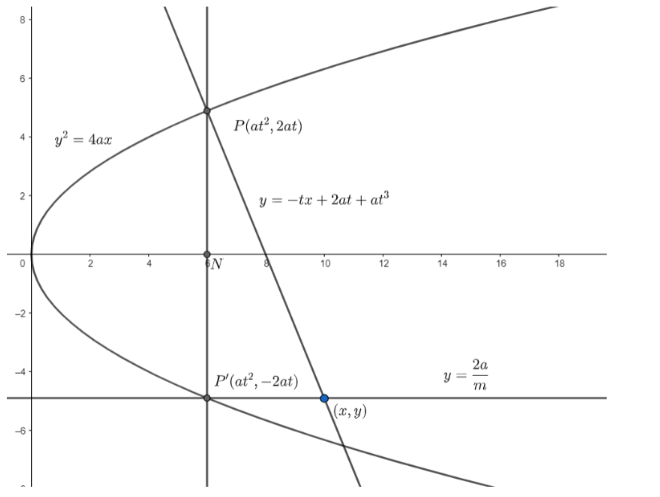
First , we need to find the equation of normal at $P$.
We know the parametric coordinates of any point on the parabola can be written as $P\left( a{{t}^{2}},2at \right)$.
Now , we know that a double ordinate is a chord which is perpendicular to the axis of the parabola .
So , the double ordinate of the point $P\left( a{{t}^{2}},2at \right)$ will be ${{P}^{'}}\left( a{{t}^{2}},-2at \right)$.
Now , we will find the equation of normal at $P$.
We know, the equation of normal at $\left( a{{t}^{2}},2at \right)$ is given as $y=-tx+2at+a{{t}^{3}}$
So , the equation of normal at $P$ is given as $y=-tx+2at+a{{t}^{3}}....\left( i \right)$
Now, we will find the equation of diameter at ${{P}^{'}}$.
We know, the general equation of diameter is given as $y=\dfrac{2a}{m}.....(ii)$, where $m$ is the slope of the diameter.
Now , we will find the point of intersection of the normal and the diameter . Let this point be $(x,y)$ .
In the question , it is given that the diameter passes through ${{P}^{'}}$.
So , we will substitute $y=-2at$ in equation $(ii)$.
On substituting $y=-2at$ in $y=\dfrac{2a}{m}$, we get
$-2at=\dfrac{2a}{m}$
$\Rightarrow m=\dfrac{-1}{t}$
Now, we will substitute $m=\dfrac{-1}{t}$ in $(ii)$. So, we get,
On substituting $m=\dfrac{-1}{t}$ in $(ii)$, we get,
$y=-2at.....\left( iii \right)$
Substituting $y=-2at$ in $\left( i \right)$, we get
$-2at=-tx+2at+a{{t}^{3}}$
Or, $tx=4at+a{{t}^{3}}$
Or, $x=4a+a{{t}^{2}}....\left( iv \right)$
Now , from $\left( iii \right)$, we have
$t=\dfrac{-y}{2a}$
Now , we will substitute $t=\dfrac{-y}{2a}$ in equation $\left( iv \right)$.
On substituting $t=\dfrac{-y}{2a}$ in equation $\left( iv \right)$, we get
$x=4a+a{{\left( \dfrac{-y}{2a} \right)}^{2}}$
$\Rightarrow x-4a=\dfrac{{{y}^{2}}}{4a}$
$\Rightarrow {{y}^{2}}=4a\left( x-4a \right)$
Hence , the locus of the point of intersection of the normal at $P$ and the diameter through ${{P}^{'}}$ is equal to the parabola ${{y}^{2}}=4a\left( x-4a \right)$.

Note: While substituting the values of $m$ and $t$, make sure the signs are correct. Students generally get confused in signs and make a mistake.