Question

PN is an ordinate of the parabola ; a straight line is drawn parallel to the axis to bisect NP and meets the curve in Q ; prove that NQ meets the tangent at the vertex in appoint T such that ${\text{AT = }}\dfrac{2}{3}{\text{NP}}$, where A is the vertex.

Answer 1

To solve this question we will first draw a figure according to the conditions given in the question. After it, we proceed by finding the coordinates of points P, N and Q. We will also use the formula to find the equation of line NQ. The formula is $({\text{y - }}{{\text{y}}_1}) = {\text{ }}\dfrac{{({{\text{y}}_2}{\text{ - }}{{\text{y}}_1})}}{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}}({\text{x - }}{{\text{x}}_1})$.

Complete step by step answer:
Now it is given that PN is the ordinate of the parabola. Let the equation of parabola be ${{\text{y}}^2}{\text{ = 4ax}}$. Also, A is the vertex of the parabola. So, we will draw the figure according to the question.
The figure of parabola is shown below.

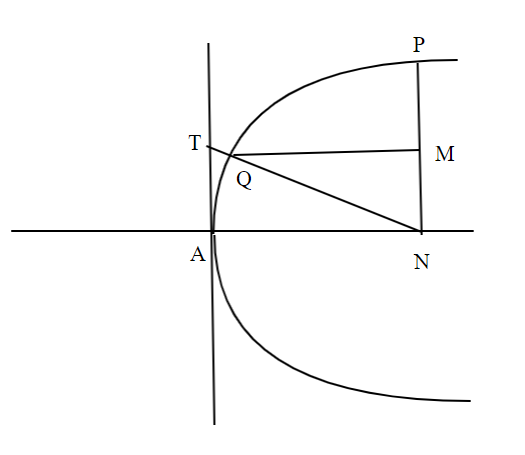
In this figure the coordinates of P are $({\text{a}}{{\text{t}}^2},{\text{ 2at)}}$ and that of C are $({\text{a}}{{\text{t}}^2},{\text{ 0)}}$. A is the vertex of parabola and it is at origin, so its coordinates are (0,0). Also, QM bisects PN so the coordinates of M are $({\text{a}}{{\text{t}}^2},{\text{ at)}}$. So, the equation of line QM is y = at. Since, QM cuts the parabola at point Q so, it must satisfy the equation of parabola. So, putting value of y in the equation of parabola, we get
${\text{x = }}\dfrac{{{\text{a}}{{\text{t}}^2}}}{4}{\text{ }}$
So, coordinates of Q are $(\dfrac{{{\text{a}}{{\text{t}}^2}}}{4}{\text{, at) }}$
Now, the line NQ meets the tangent of parabola at point T. So, equation of line NQ is
${\text{y - y}}{}_1{\text{ = }}\dfrac{{{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}}}{{{{\text{x}}_2}{\text{ - }}{{\text{x}}_1}}}({\text{x - }}{{\text{x}}_1})$
Applying value in the above equation we get
${\text{y = }}\dfrac{{ - 4}}{{3{\text{t}}}}({\text{x - a}}{{\text{t}}^2})$
Now the point T lies on y – axis, so its x - coordinate = 0. So,
${\text{y = }}\dfrac{{4{\text{at}}}}{3}$
So, the coordinates of point T are $(0,{\text{ }}\dfrac{{4{\text{at}}}}{3})$.
Now length of PN = $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}}$ = $2{\text{at}}$
Similarly, length of AT = $\dfrac{{4{\text{at}}}}{3}$

So, ${\text{AT = }}\dfrac{2}{3}{\text{NP}}$. Hence proved.

Note: When we come up with such a type of question, we will follow a few steps to solve the given problem. First, we will draw a figure with the help of given conditions in the question. After it, we will find the required coordinates and equations of lines to solve the question. While finding the equation of a line we have to use the formula $({\text{y - }}{{\text{y}}_1}) = {\text{ }}\dfrac{{({{\text{y}}_2}{\text{ - }}{{\text{y}}_1})}}{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}}({\text{x - }}{{\text{x}}_1})$. Most students make mistakes by applying the incorrect formula. Carefully apply the formula to get the correct answer.