Solveeit Logo
Login

Question

Question: Plot the graph of \({{\sin }^{-1}}\left( \sin x \right)\) and write its domain and range....

Plot the graph of sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right) and write its domain and range.

Explanation

Solution

To draw the graph of sin⁡−1(sin⁡x){{\sin }^{-1}}\left( \sin x \right), we must know about the following concepts,
Inverse of a function means a function which returns back the original value applied on the given function. Inverse of a particular function exists if the function is bijective.i.e., for each unique value from the domain of the function, we should have a corresponding unique value from the range of the function.

Complete step-by-step solution:
For a function ff , if its inverse exists, then
f−1(f(x))=x where x∈Range of f−1(x){{f}^{-1}}\left( f\left( x \right) \right)=x\text{ where }x\in Range\text{ of }{{f}^{-1}}\left( x \right)
Another point to be noted is
If, sin⁡y=sin⁡x ⇒y=nπ+(−1)nx \begin{aligned} & \text{If, }\sin y=\sin x \\\ & \Rightarrow y=n\pi +{{\left( -1 \right)}^{n}}x \\\ \end{aligned}
Range of y=sin⁡−1xy={{\sin }^{-1}}x ∀x∈(−1,1),y∈(−π2,π2)\forall x\in \left( -1,1 \right),y\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)
Now, let us proceed with the question,
We have, f(x)=sin⁡−1(sin⁡x)f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)
Let us assume f(x)=θf\left( x \right)=\theta
⇒sin⁡−1(sin⁡x)=θ ⇒sin⁡x=sin⁡θ \begin{aligned} & \Rightarrow {{\sin }^{-1}}\left( \sin x \right)=\theta \\\ & \Rightarrow \sin x=\sin \theta \\\ \end{aligned}
Using,
If, sin⁡y=sin⁡x ⇒y=nπ+(−1)nx \begin{aligned} & \text{If, }\sin y=\sin x \\\ & \Rightarrow y=n\pi +{{\left( -1 \right)}^{n}}x \\\ \end{aligned}
We get
⇒θ=nπ+(−1)nx\Rightarrow \theta =n\pi +{{\left( -1 \right)}^{n}}x
For different values of xx , we will get different values of θ\theta .i.e., for different values of xx, we will get different values of f(x)f\left( x \right) .
For n=−1n=-1
θ=sin⁡−1(sin⁡(−π−x))\theta ={{\sin }^{-1}}\left( \sin \left( -\pi -x \right) \right)
For θ\theta to exist,
−π2≤−π−x≤π2 ⇒π2≤−x≤3π2 ⇒−π2≥x≥−3π2 \begin{aligned} & \dfrac{-\pi }{2}\le -\pi -x\le \dfrac{\pi }{2} \\\ & \Rightarrow \dfrac{\pi }{2}\le -x\le \dfrac{3\pi }{2} \\\ & \Rightarrow \dfrac{-\pi }{2}\ge x\ge \dfrac{-3\pi }{2} \\\ \end{aligned}
For n=0,n=0,
θ=sin⁡−1(sin⁡x)\theta ={{\sin }^{-1}}\left( \sin x \right)
For θ\theta to exist,
−π2≤x≤π2\dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2}
For n=1,n=1,
θ=sin⁡−1(sin⁡(π−x))\theta ={{\sin }^{-1}}\left( \sin \left( \pi -x \right) \right)
For θ\theta to exist,
−π2≤π−x≤π2 ⇒−3π2≤−x≤−π2 ⇒3π2≥x≥π2 \begin{aligned} & \dfrac{-\pi }{2}\le \pi -x\le \dfrac{\pi }{2} \\\ & \Rightarrow \dfrac{-3\pi }{2}\le -x\le \dfrac{-\pi }{2} \\\ & \Rightarrow \dfrac{3\pi }{2}\ge x\ge \dfrac{\pi }{2} \\\ \end{aligned}
So, we can redefine the function f(x)f\left( x \right) as
f\left( x \right)=\left\\{ \begin{matrix} & -\pi -x &\dfrac{-3\pi }{2}\le x\le \dfrac{-\pi }{2} \\\ & x & \dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2} \\\ & \pi -x & \dfrac{\pi }{2}\le x\le \dfrac{3\pi }{2} \\\ \end{matrix} \right.
Now, using these inequalities we will draw the graph of f(x)=sin⁡−1(sin⁡x)f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)

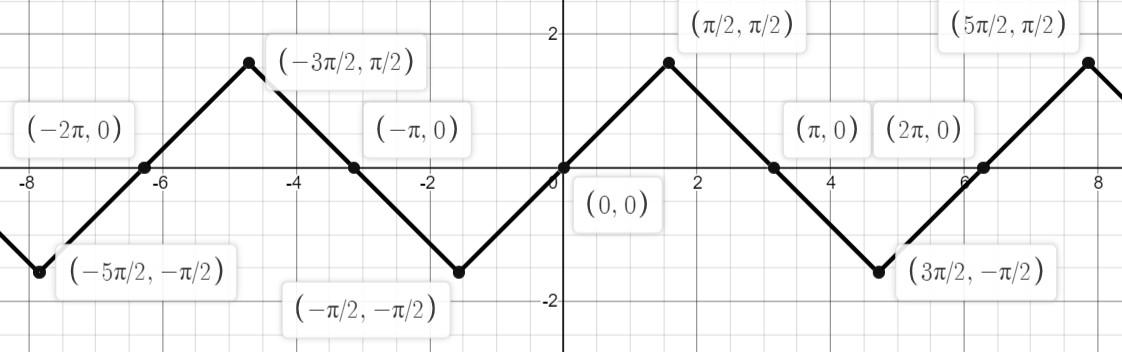
So, for the function f(x)=sin⁡−1(sin⁡x)f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)
Domain:x∈RDomain:x\in R
Range:x∈(−π2,π2)Range:x\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)
The graph is periodic with a fundamental period of 2π2\pi .

Note: While drawing the graph of f(x)=sin⁡−1(sin⁡x)f\left( x \right)={{\sin }^{-1}}\left( \sin x \right), remember that the different values of xx should correspond to the range of sin⁡−1x{{\sin }^{-1}}x .i.e.,x∈(−π2,π2)x\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right). Here, since xx is the domain of sin⁡x\sin x, hence x∈Rx\in R. This means that sin⁡x∈(−1,1)\sin x\in \left( -1,1 \right) and hence sin⁡−1(sin⁡x)∈(−π2,π2){{\sin }^{-1}}\left( \sin x \right)\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right). So, the given function has a range of (−π2,π2)\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right) for every x∈Rx\in R.