Question
Question: Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate ...
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: ( x is in cm and t is in sec ).
(A). x=−2sin(3t+3π)
(B). x=cos(6π−t)
(C). x=3sin(2πt+4π)
(D). x=2cosπt
Solution
You can start the solution by defining what simple harmonic motion is. Then define the standard equation for simple harmonic motion, i.e. x=Acos(T2πt+ϕ). Then compare this equation with all of the four cases converting all of the equations in the cos form.
Complete step by step answer:
Simple Harmonic Motion – It is a periodic motion which is caused due to a restoring force which is directly proportional to the distance of the object from the mean position and the direction of this force is always towards the equilibrium position.
In the problem we are given four particles and their respective SHM equation. The standard SHM equation is
x=Acos(T2πt+ϕ)
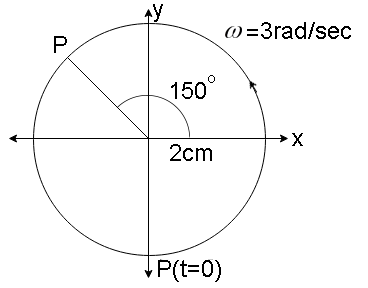
(A). x=−2sin(3t+3π)=2cos(3t+3π+2π)
Comparing this equation with the standard SHM equation,
x=Acos(T2πt+ϕ)
Amplitude A=2cm
Phase angle ϕ=65π
Angular velocity ω=T2π=3rad/sec
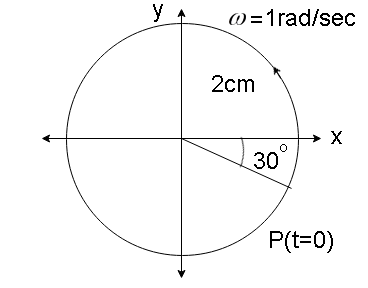
(b) x=cos(6π−t)=cos(t−6π)
Comparing this equation with the standard SHM equation
Amplitude A=1
Phase angle ϕ=−6π
Angular velocity ω=T2π=1rad/sec
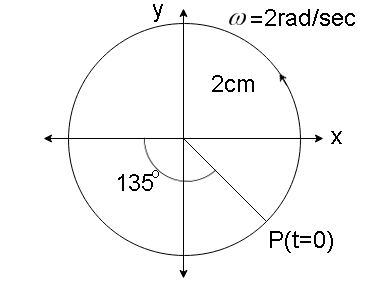
(c) x=3sin(2πt+4π)
=−cos[(2πt+4π)+2π]=−3cos(2πt+43π)
Comparing this equation with the standard SHM equation
Amplitude A=3cm
Phase angle ϕ=43π
Angular velocity ω=T2π=2πrad/sec
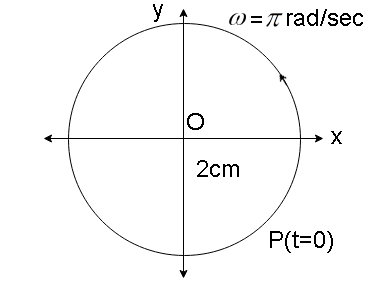
(d) x=2cosπt
Comparing this equation with the standard SHM equation
AmplitudeA=2cm
Phase angle ϕ=0
Angular velocity ω=T2π=πrad/sec
Note:
Simple harmonic motion is a great example of conservation of energy. When the object from its equilibrium position it only has potential energy. While reaching the extreme positions this energy is converted into kinetic energy and then again back into potential energy as the objects start moving back to equilibrium.
