Question

Plot $A \times B$ and $B \times A$ on XY-plane if: A = \left\\{ {x:x \in N,1 \le x \le 5} \right\\} and B = \left\\{ {y:y \in W,y < 3} \right\\}.

Answer 1

Here, we need to plot the Cartesian products. First, we will write the sets in roster form. Then, we will find their Cartesian products. Finally, we will plot the ordered pairs in the Cartesian products on the XY plane.

Complete step-by-step answer:
The given sets A = \left\\{ {x:x \in N,1 \le x \le 5} \right\\} and B = \left\\{ {y:y \in W,y < 3} \right\\} are in set-builder form.
We will rewrite the sets A and B using the roster method.
First, let us find the elements of set A.
The value of $x$ in set A = \left\\{ {x:x \in N,1 \le x \le 5} \right\\} is any natural number between 1 and 5, both included.
The possible values of $x$ are 1, 2, 3, 4, 5.
Therefore, we can rewrite set A using roster method as
A = \left\\{ {1,2,3,4,5} \right\\}
Next, we will find the elements of set B.
The value of $y$ in set B = \left\\{ {y:y \in W,y < 3} \right\\} is any whole number less than 3.
The possible values of $y$ are 0, 1, 2.
Therefore, we can rewrite set B using roster method as
B = \left\\{ {0,1,2} \right\\}
Now, we will find the Cartesian product $A \times B$.
The Cartesian product $A \times B$ of two sets A and B is the set of all possible ordered pairs $\left( {x,y} \right)$, where $x \in A$ and $y \in B$.
The first component $x$ of ordered pair $\left( {x,y} \right)$ in the Cartesian product $A \times B$ can be 1, 2, 3, 4, or 5, because A = \left\\{ {1,2,3,4,5} \right\\}.
The second component $y$ of ordered pair $\left( {x,y} \right)$ in the Cartesian product $A \times B$ can be 0, 1, or 2, because B = \left\\{ {0,1,2} \right\\}.
Therefore, we get the Cartesian product $A \times B$ as
A \times B = \left\\{ \begin{array}{l}\left( {1,0} \right),\left( {2,0} \right),\left( {3,0} \right),\left( {4,0} \right),\left( {5,0} \right),\left( {1,1} \right),\left( {2,1} \right),\left( {3,1} \right),\\\\\left( {4,1} \right),\left( {5,1} \right),\left( {1,2} \right),\left( {2,2} \right),\left( {3,2} \right),\left( {4,2} \right),\left( {5,2} \right)\end{array} \right\\}
Now, we will plot the ordered pairs $\left( {x,y} \right)$ of the Cartesian product $A \times B$ on the XY-plane.
Plotting the points, we get the graph as

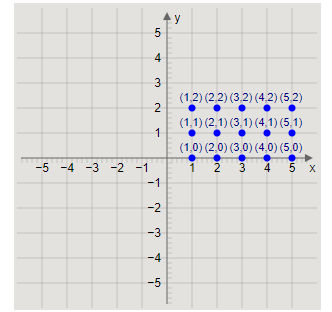
Now, we will find the Cartesian product $B \times A$.
The Cartesian product $B \times A$ of two sets A and B is the set of all possible ordered pairs $\left( {y,x} \right)$, where $y \in B$ and $x \in A$.
The first component $y$ of ordered pair $\left( {y,x} \right)$ in the Cartesian product $B \times A$ can be 0, 1, or 2, because B = \left\\{ {0,1,2} \right\\}.
The second component $x$ of ordered pair $\left( {y,x} \right)$ in the Cartesian product $B \times A$ can be 1, 2, 3, 4, or 5, because A = \left\\{ {1,2,3,4,5} \right\\}.
Therefore, we get the Cartesian product $B \times A$ as
B \times A = \left\\{ \begin{array}{l}\left( {0,1} \right),\left( {1,1} \right),\left( {2,1} \right),\left( {0,2} \right),\left( {1,2} \right),\left( {2,2} \right),\left( {0,3} \right),\left( {1,3} \right),\\\\\left( {2,3} \right),\left( {0,4} \right),\left( {1,4} \right),\left( {2,4} \right),\left( {0,5} \right),\left( {1,5} \right),\left( {2,5} \right)\end{array} \right\\}
Now, we will plot the ordered pairs $\left( {y,x} \right)$ of the Cartesian product $B \times A$ on XY-plane.
Plotting the points, we get the graph as

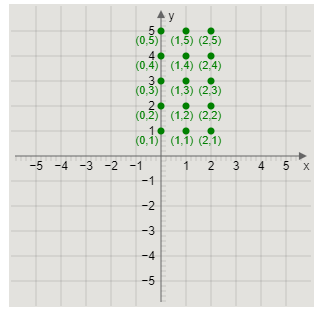
Note: We rewrite the sets A and B using roster method. A set is said to be written using roster method if all the elements of the set are written.
We used the terms ‘whole number’ and ‘natural number’ in the solution.
Whole numbers include the numbers 0, and all the positive integers like 1, 2, 3, etc. They are the basic numbers we use when counting objects.
For example: 0, 1, 2, 100, 400, 52225, are all whole numbers.
Natural numbers include all the positive integers like 1, 2, 3, etc.
For example: 1, 2, 100, 400, 52225, are all whole numbers.
Whole numbers include all the natural numbers, and the number 0.