Question

The statement "$ab = ac \Rightarrow b=c$" asserts that if the product of $a$ with $b$ is equal to the product of $a$ with $c$, then $b$ must be equal to $c$. This implication is false in general.

The provided derivation shows the reasoning: Starting with the equation: $ab = ac$

Subtract $ac$ from both sides: $ab - ac = 0$

Factor out the common term $a$: $a(b-c) = 0$

For the product of two quantities to be zero, at least one of the quantities must be zero. This leads to two possibilities:

1. $a = 0$
2. $b-c = 0$ (which implies $b=c$)

The implication "$ab = ac \Rightarrow b=c$" is only true if the second case ($b-c=0$) is the only possible outcome. However, the first case ($a=0$) shows that this is not always true.

Counterexample: If $a=0$, the equation $a(b-c)=0$ becomes $0 \cdot (b-c) = 0$, which simplifies to $0=0$. This equation is true for any values of $b$ and $c$. Therefore, if $a=0$, $b$ does not necessarily have to be equal to $c$.

For instance, let $a=0$, $b=5$, and $c=10$. Then, $ab = 0 \times 5 = 0$. And $ac = 0 \times 10 = 0$. So, $ab = ac$ is true ($0=0$). However, $b \neq c$ ($5 \neq 10$). This counterexample demonstrates that the statement "$ab = ac \Rightarrow b=c$" is false.

The note "Do not cancel the common terms from both sides. We can cancel only if a is non zero" highlights the pitfall. Cancelling $a$ from $ab=ac$ (which is equivalent to dividing by $a$) is only a valid operation if $a \neq 0$. If $a$ can be zero, then cancelling it would lead to an incorrect conclusion that $b=c$ always follows, ignoring the case where $a=0$ and $b \neq c$.

The implication "$ab = ac \Rightarrow b=c$" holds true only under the condition that $a \neq 0$.

---

Explanation of the solution (minimal)

The statement $ab = ac \Rightarrow b=c$ is false. Rearranging $ab=ac$ gives $a(b-c)=0$. This implies $a=0$ or $b-c=0$. If $a=0$, $b$ need not equal $c$ (e.g., $a=0, b=5, c=10$). The conclusion $b=c$ is only guaranteed if $a \neq 0$.

Answer 1

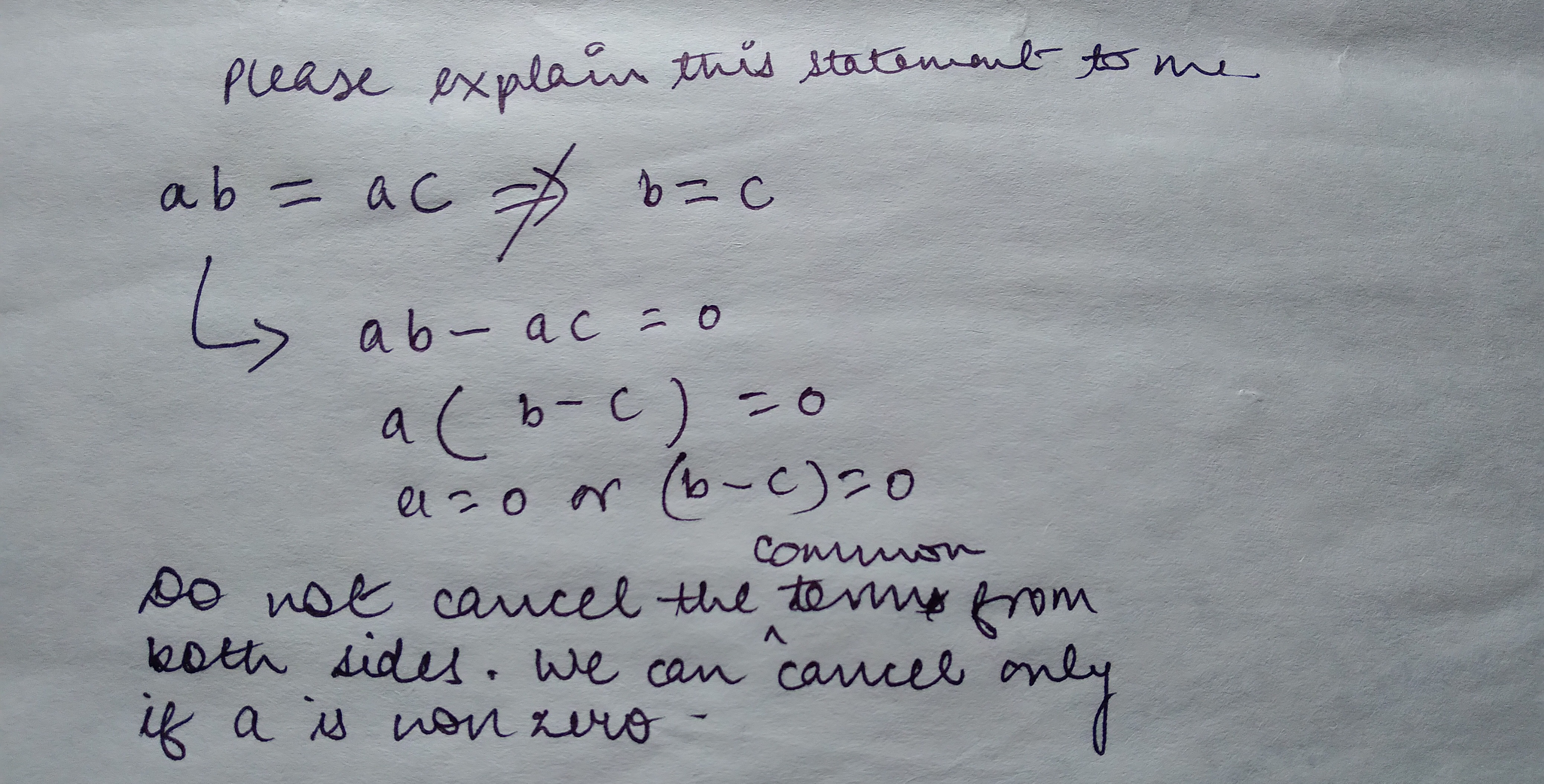
The statement is False.

Answer 2

The statement $ab = ac \Rightarrow b=c$ is false. Rearranging $ab=ac$ gives $a(b-c)=0$. This implies $a=0$ or $b-c=0$. If $a=0$, $b$ need not equal $c$ (e.g., $a=0, b=5, c=10$). The conclusion $b=c$ is only guaranteed if $a \neq 0$.