Question

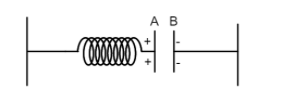
Plate A of a parallel air-filled capacitor is connected to a non-conducting spring having force constant $k$ and the plate $B$ Is fixed. If a charge $+ {\text{ }}q$ is placed on plate $A$ and charge $-q$ on the plate $B$ then find out an extension in the spring in equilibrium. Assume the area of the plate is $'A'$.

Answer 1

-The spring is expanded by the attraction force between the two plates.
-Find the electrostatic force from the stored potential energy of the capacitor.
-The electrostatic force is equal to the attraction force between the two plates. Find the expanded length of the spring using the force constant.

Formula used:
the attraction force $F = - kl$
Where,
$k$is the force constant of the spring and $l$ is the expanded length of the spring.
The stored potential energy $U = \dfrac{1}{2}\dfrac{{{q^2}}}{C}$
Where, $q$ is the charge on the capacitor, and $C$ is the capacitance.
$C = \dfrac{{{\varepsilon _0}A}}{y}$
where,
$A$ is the area of the plate,
${\varepsilon _0}$ is the permittivity in air medium,
$y$ is the distance between two parallel plates.
The electrostatic force of the capacitor $F = \dfrac{{dU}}{{dy}}$

Complete step by step answer:
The spring is attached with a parallel plate capacitor and is expanded to a certain length due to the attraction force of the capacitor.

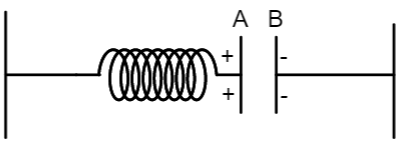
Now, the attraction force $F = - kl...............(1)$
Where,
$k$is the force constant of the spring and $l$ is the expanded length of the spring.
Now, if the area of the plates is $A$ and $y$ is the distance between two parallel plates,
The capacitance, $C = \dfrac{{{\varepsilon _0}A}}{y}...............(2)$, ${\varepsilon _0}$ is the permittivity in air medium,
We know, The stored potential energy $U = \dfrac{1}{2}\dfrac{{{q^2}}}{C}.................(3)$
Where, $q$ is the charge on the capacitor, and $C$ is the capacitance.
From eq. $(2)$ we can write, $U = \dfrac{1}{2}\dfrac{{{q^2}y}}{{{\varepsilon _0}A}}$ [putting the value of $C$]
Since the electrostatic force is conservative, it can be written as the
$F = - \dfrac{{dU}}{{dy}}$
$F = - \dfrac{d}{{dy}}\left( {\dfrac{1}{2}\dfrac{{{q^2}y}}{{{\varepsilon _0}A}}} \right)$
$\Rightarrow F = - \dfrac{1}{2}\dfrac{{{q^2}}}{{{\varepsilon _0}A}}.....................(4)$ [ the negative sign implies the attraction force]
From $(1)$ and $(4)$ we get,
$- kl = - \dfrac{1}{2}\dfrac{{{q^2}}}{{{\varepsilon _0}A}}$
$\Rightarrow kl = \dfrac{1}{2}\dfrac{{{q^2}}}{{{\varepsilon _0}A}}$
$\Rightarrow l = \dfrac{1}{2}\dfrac{{{q^2}}}{{{\varepsilon _0}Ak}}$
Hence the extension in the spring is, $\Rightarrow l = \dfrac{1}{2}\dfrac{{{q^2}}}{{{\varepsilon _0}Ak}}$.

Note: The electrostatic force is taken, $F = - \dfrac{{dU}}{{dy}}$
This defines that the electrostatic force is conservative and is the negative gradient of the potential. The potential is the work done. We know to charge a capacitor the required work is stored as potential energy in the capacitor.
Hence the force is taken as the gradient of the stored potential energy of the capacitor.