Question

Pitch of the helical path described by the particle is:
$\text{A}\text{. }\dfrac{2\pi m{{v}_{o}}}{{{B}_{o}}q}$
$\text{B}\text{. }\dfrac{\sqrt{3}\pi m{{v}_{o}}}{2{{B}_{o}}q}$
$\text{C}\text{. }\dfrac{\pi m{{v}_{o}}}{{{B}_{o}}q}$
$\text{D}\text{. }\dfrac{2\sqrt{3}\pi m{{v}_{o}}}{{{B}_{o}}q}$

Answer 1

Hint : When a charged particle goes through a region of magnetic field, two different forces act on it. First one is the force exerted on charged particles due to the magnetic field and the other force is centripetal force. The velocity of a particle is constant in the direction parallel to the magnetic field and the motion is accelerating in the direction perpendicular to the magnetic field. We will find the expression for velocity, time period and pitch of the helical path described by the particle.
Formula used:

Magnetic force,${{F}_{B}}=q\left( v\times B \right)$
Centripetal force,${{F}_{C}}=m\dfrac{{{v}^{2}}}{r}$

Complete step by step answer:
Suppose that a charged particle of mass $m$moves in a circular orbit of radius$r$, with a constant speed$v$. The acceleration of the particle is of magnitude $\dfrac{m{{v}^{2}}}{r}$, and is always directed towards the center of the orbit. It follows that the acceleration of the particle is always perpendicular to the particle’s instantaneous direction of motion.
Also, force exerted on the moving charge under the magnetic field is given by, $q\left( v\times B \right)$. The direction of the magnetic force is always perpendicular to the instantaneous direction of motion.

A charged particle placed in a magnetic field executes a circular orbit in the plane perpendicular to the direction of the field. Since, the magnetic force on the particle $q\left( v\times B \right)$ depends on the component of particle’s which is perpendicular to the direction of magnetic field. The combination of circular motion in the plane perpendicular to the magnetic field, and uniform motion along the direction of magnetic field, gives rise to a spiral trajectory of a charged particle in a magnetic field, where the field forMS the axis of the spiral.

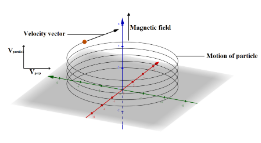
Magnetic force acting on the particle having charge $+q$ is given by,
${{F}_{B}}=q\left( v\times B \right)$
Where,
$v$ is the velocity of the charged particle moving perpendicular to the magnetic field
$B$ is the magnetic field intensity
The magnetic force on a charged particle acts perpendicular to both the velocity and magnetic field.

Magnitude of magnetic force is given as,
${{F}_{B}}=qvB$
Centripetal force on charged particle,
${{F}_{C}}=m\dfrac{{{v}^{2}}}{r}$
Where,
$m$ is the mass of the particle
$v$ is the velocity of the particle
$r$ is the radius of circular path of the particle
Since, charged particle is assumed to have a constant speed in the region parallel to the magnetic field,
Therefore, magnetic force should be equal to centripetal force

${{F}_{B}}={{F}_{C}}$
$qvB=m\dfrac{{{v}^{2}}}{r}$
$r=\dfrac{mv}{qB}$

Time taken by the particle to complete one full oscillation, that is, time period of the oscillation is,

$T=\dfrac{2\pi r}{v}$

Pitch is the distance moved by the particle along the direction of magnetic field in one rotation,

$P={{v}_{o}}T$

Where,

${{v}_{o}}$is the velocity of charged particle parallel to the magnetic field
$P=\dfrac{2\pi m}{qB}{{v}_{o}}$
Pitch of the helical path described by the particle is $\dfrac{2\pi m}{qB}{{v}_{o}}$
Hence, the correct option is A.

Note :
Motion of charged particles is accelerating, circular motion, in the direction perpendicular to the magnetic field. But, in the direction parallel to the magnetic field, the particle moves with a constant speed because the magnetic field applies force only in the direction perpendicular to it. Thus, the force cannot do work on the particle, meaning that there is no change in its kinetic energy and therefore, the particle moves with a constant speed in the direction parallel to the magnetic field.