Question

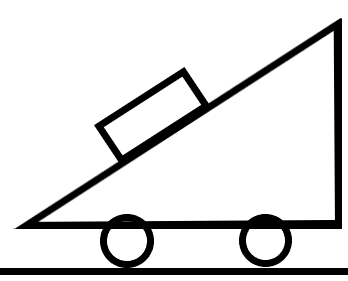
Picture a cart with an inclined top surface (see diagram). Assume $\theta ={{30}^{0}}$. At what rate must the cart accelerate to the slide to keep a frictionless block on it from sliding off (in $m{{s}^{-2}}$)?

A) 4.9
B) 5.7
C) 8.5
D) 17.0

Answer 1

We need to understand the relation of the acceleration that will be acting on the cart which can keep a box without sliding down the frictionless contact between the cart and the block. We can relate the gravitational force and the external force.

Complete step-by-step solution
We are given a situation in which a cart with an inclined top surface is accelerating in a direction with a box kept on the inclined plane. The contact between the box and the cart is such that there exists no friction between the two surfaces. So, we can understand that for the box not to be sliding down the plane, there should be acceleration along the horizontal.

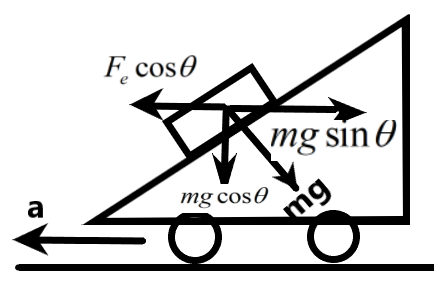
We know that for a body undergoing acceleration, a force will be acting on it. Also, the gravitational force acts along the vertical direction of the system. We can resolve the components of both the forces and equate the horizontal components to get the required acceleration.
i.e.,

& {{F}_{g}}\sin \theta ={{F}_{e}}\cos \theta \\\ & \Rightarrow mg\sin \theta =ma\cos \theta \\\ & \Rightarrow g\sin {{30}^{0}}=a\cos {{30}^{0}} \\\ & \Rightarrow (9.8)\dfrac{1}{2}=a(\dfrac{\sqrt{3}}{2}) \\\ & \therefore a=5.66m{{s}^{-2}} \\\ \end{aligned}$$ The acceleration produced by the cart so that the box placed on its inclined plane will be at rest without sliding is at 5.7 $$m{{s}^{-2}}$$. This is the required solution. **The correct answer is option B.** **Note:** The external force acting on the body is completely balancing the box on the inclined surface. In practical situations, the frictional force between the cart and the box is necessary to keep the box from sliding depending on the angle of inclination.