Solveeit Logo
Login

Question

Question: $\Pi$ 1. $\int_{0.5}^{1} \frac{dx}{1+e^{x}}$...

Π\Pi

  1. ∫0.51dx1+ex\int_{0.5}^{1} \frac{dx}{1+e^{x}}
Answer

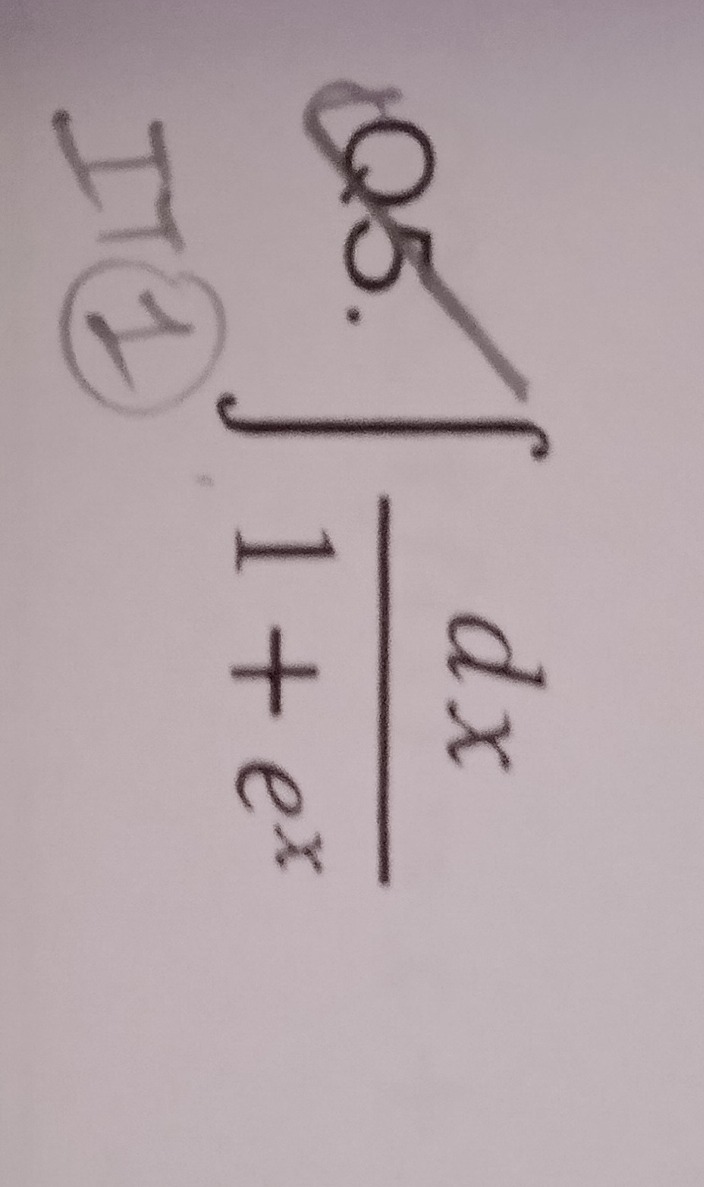
0.5 + ln((1+e^{0.5})/(1+e))

Explanation

Solution

The problem requires evaluating a definite integral. First, we find the indefinite integral of the given function, and then apply the limits of integration.

1. Find the indefinite integral ∫dx1+ex\int \frac{dx}{1+e^x}

We can use the substitution method or algebraic manipulation. Multiply the numerator and denominator by e−xe^{-x}: I=∫dx1+ex=∫e−xdxe−x(1+ex)=∫e−xdxe−x+1I = \int \frac{dx}{1+e^x} = \int \frac{e^{-x} dx}{e^{-x}(1+e^x)} = \int \frac{e^{-x} dx}{e^{-x}+1} Let u=e−x+1u = e^{-x}+1. Differentiating uu with respect to xx, we get du=−e−xdxdu = -e^{-x} dx. So, e−xdx=−due^{-x} dx = -du. Substitute these into the integral: I=∫−duu=−∫1udu=−ln⁡∣u∣+CI = \int \frac{-du}{u} = -\int \frac{1}{u} du = -\ln|u| + C Substitute back u=e−x+1u = e^{-x}+1: I=−ln⁡(e−x+1)+CI = -\ln(e^{-x}+1) + C Since e−x+1=1ex+1=1+exexe^{-x}+1 = \frac{1}{e^x}+1 = \frac{1+e^x}{e^x}, we can rewrite the expression: I=−ln⁡(1+exex)+CI = -\ln\left(\frac{1+e^x}{e^x}\right) + C Using the logarithm property ln⁡(ab)=ln⁡a−ln⁡b\ln\left(\frac{a}{b}\right) = \ln a - \ln b: I=−(ln⁡(1+ex)−ln⁡(ex))+CI = -(\ln(1+e^x) - \ln(e^x)) + C I=−ln⁡(1+ex)+ln⁡(ex)+CI = -\ln(1+e^x) + \ln(e^x) + C Since ln⁡(ex)=x\ln(e^x) = x: I=x−ln⁡(1+ex)+CI = x - \ln(1+e^x) + C

2. Evaluate the definite integral

Now, we apply the limits of integration from 0.50.5 to 11: ∫0.51dx1+ex=[x−ln⁡(1+ex)]0.51\int_{0.5}^{1} \frac{dx}{1+e^{x}} = [x - \ln(1+e^x)]_{0.5}^{1} Using the Fundamental Theorem of Calculus, F(b)−F(a)F(b) - F(a): =(1−ln⁡(1+e1))−(0.5−ln⁡(1+e0.5))= (1 - \ln(1+e^1)) - (0.5 - \ln(1+e^{0.5})) =1−ln⁡(1+e)−0.5+ln⁡(1+e0.5)= 1 - \ln(1+e) - 0.5 + \ln(1+e^{0.5}) Combine the constant terms and the logarithm terms: =(1−0.5)+(ln⁡(1+e0.5)−ln⁡(1+e))= (1 - 0.5) + (\ln(1+e^{0.5}) - \ln(1+e)) =0.5+ln⁡(1+e0.51+e)= 0.5 + \ln\left(\frac{1+e^{0.5}}{1+e}\right)