Question

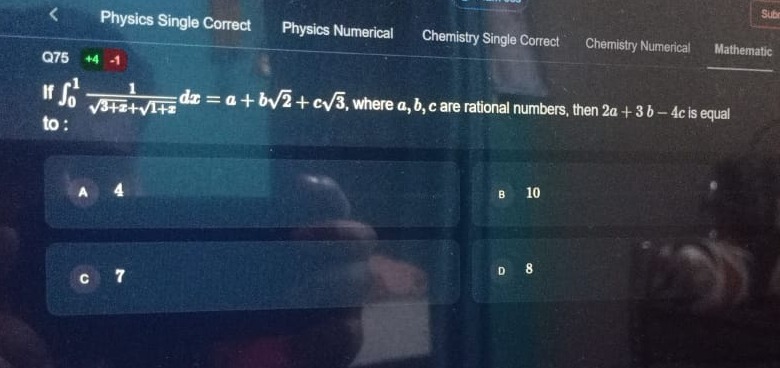
If $\int_{0}^{1} \frac{1}{\sqrt{3+x}+\sqrt{1+x}} dx = a + b\sqrt{2} + c\sqrt{3}$, where a, b, c are rational numbers, then $2a + 3b - 4c$ is equal to :

• A. 4
• B. 10
• C. 7
• D. 8

Answer 1

Answer: (D)

8

Answer 2

Here's how to solve this definite integral problem:

1. Rationalize the Integrand

Multiply the numerator and denominator by the conjugate:

$\frac{1}{\sqrt{3+x}+\sqrt{1+x}} \cdot \frac{\sqrt{3+x}-\sqrt{1+x}}{\sqrt{3+x}-\sqrt{1+x}} = \frac{\sqrt{3+x}-\sqrt{1+x}}{2}$

2. Evaluate the Definite Integral

$\int_{0}^{1} \frac{\sqrt{3+x}-\sqrt{1+x}}{2} dx = \frac{1}{2} \int_{0}^{1} (\sqrt{3+x} - \sqrt{1+x}) dx$

Using the power rule for integration:

$= \frac{1}{2} \left[ \frac{2}{3}(3+x)^{3/2} - \frac{2}{3}(1+x)^{3/2} \right]_{0}^{1}$

$= \frac{1}{3} \left[ (3+x)^{3/2} - (1+x)^{3/2} \right]_{0}^{1}$

Evaluate at the limits:

$= \frac{1}{3} \left[ (4^{3/2} - 2^{3/2}) - (3^{3/2} - 1^{3/2}) \right]$

$= \frac{1}{3} \left[ (8 - 2\sqrt{2}) - (3\sqrt{3} - 1) \right]$

$= \frac{1}{3} \left[ 9 - 2\sqrt{2} - 3\sqrt{3} \right] = 3 - \frac{2}{3}\sqrt{2} - \sqrt{3}$

3. Identify a, b, c

Comparing $3 - \frac{2}{3}\sqrt{2} - \sqrt{3}$ with $a + b\sqrt{2} + c\sqrt{3}$:

$a = 3$, $b = -\frac{2}{3}$, $c = -1$

4. Calculate $2a + 3b - 4c$

$2(3) + 3(-\frac{2}{3}) - 4(-1) = 6 - 2 + 4 = 8$