Solveeit Logo
Login

Question

Question: A concave mirror of focal length 50 cm is placed at origin as shown in diagram. A point sized object...

A concave mirror of focal length 50 cm is placed at origin as shown in diagram. A point sized object is placed at O (x = 152 cm). A glass slab of thickness 4 cm, μ\mu = 2, is placed symmetrically around C. Light can not reach from object to mirror without passing through slab. Choose the correct option(s):

A

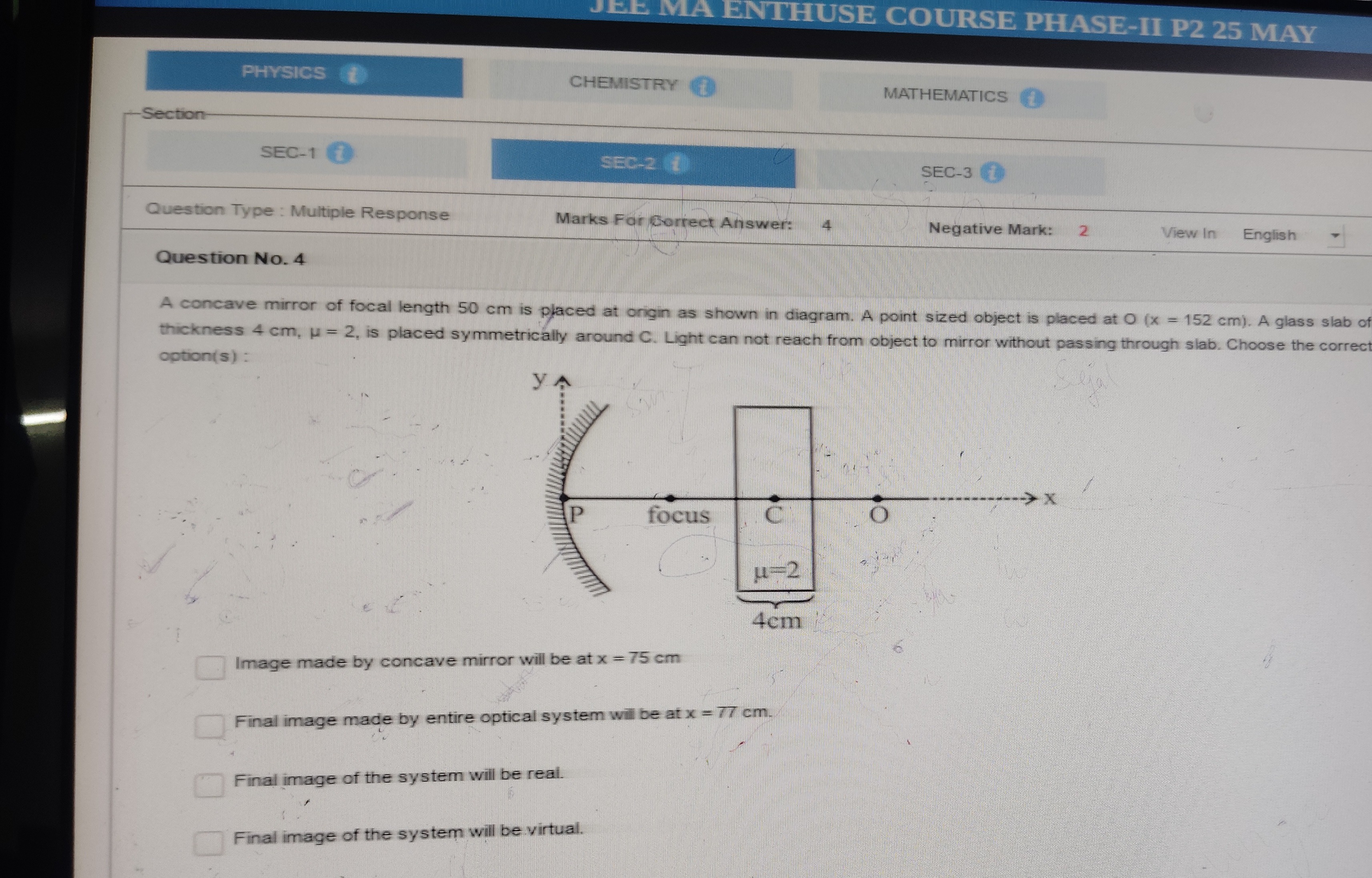
Image made by concave mirror will be at x = 75 cm

B

Final image made by entire optical system will be at x = 77 cm.

C

Final image of the system will be real.

D

Final image of the system will be virtual.

Answer

Image made by concave mirror will be at x = 75 cm, Final image made by entire optical system will be at x = 77 cm, Final image of the system will be real.

Explanation

Solution

The problem involves a concave mirror and a glass slab. Let's assume the standard sign convention where the mirror is at the origin (x=0), and the positive x-axis is to the right.

  1. Intermediate Image Formation by the Concave Mirror:

    The object is at x = 152 cm. The light passes through the glass slab of thickness 4 cm and μ=2\mu = 2. The shift due to the slab is Δx=t(1−1/μ)=4(1−1/2)=2\Delta x = t(1 - 1/\mu) = 4(1 - 1/2) = 2 cm. The apparent position of the object as seen from the mirror is shifted towards the mirror by 2 cm.

    The apparent object distance from the mirror is u=152−2=150u = 152 - 2 = 150 cm. The focal length of the concave mirror is f=50f = 50 cm. Using the mirror formula:

    1v+1u=1f\frac{1}{v} + \frac{1}{u} = \frac{1}{f}

    1v+1150=150\frac{1}{v} + \frac{1}{150} = \frac{1}{50}

    1v=150−1150=3−1150=2150=175\frac{1}{v} = \frac{1}{50} - \frac{1}{150} = \frac{3 - 1}{150} = \frac{2}{150} = \frac{1}{75}

    v=75v = 75 cm.

    The intermediate image formed by the concave mirror is at x = 75 cm. This image is real.

  2. Final Image Formation after Passing through the Slab Again:

    The intermediate image at x = 75 cm acts as the object for the return pass through the slab. The light rays from the mirror form an image at x = 75 cm. These rays pass through the slab again. The shift is Δx=t(1−1/μ)=4(1−1/2)=2\Delta x = t(1 - 1/\mu) = 4(1 - 1/2) = 2 cm.

    The final image position is at xfinal=75+2=77x_{final} = 75 + 2 = 77 cm.

  3. Nature of the Final Image:

    Since the intermediate image formed by the mirror is real, the final image formed after passing through the slab will also be real.