Solveeit Logo
Login

Question

Question: Photon with kinetic energy of \(1\,MeV\) moves from south to north. It gets an acceleration of \({10...

Photon with kinetic energy of 1 MeV1\,MeV moves from south to north. It gets an acceleration of 1012m s−2{10^{12}}m{\text{ }}{s^{ - 2}} by an applied magnetic field (west to east). The value of magnetic field: (Rest mass of proton is 1.6×10−27kg1.6 \times {10^{ - 27}}kg):
A. 0.071 mT0.071\,mT
B. 71 mT71\,mT
C. 0.71 mT0.71\,mT
D. 7.1 mT7.1\,mT

Explanation

Solution

To solve this question, one must have a concept of force acting on a magnetic field and kinetic energy then one can easily solve this question. First, we have changed the unit of kinetic energy and then found the velocity of the particle and then using Newton's law of motion we have found the value of the magnetic field and hence we got our required solution.

Formula used:
Bqv=maBqv = ma
Where, BB is the magnetic field, qq is the charge, vv is the velocity, mm is the mass and aa is the acceleration.

Complete step by step answer:

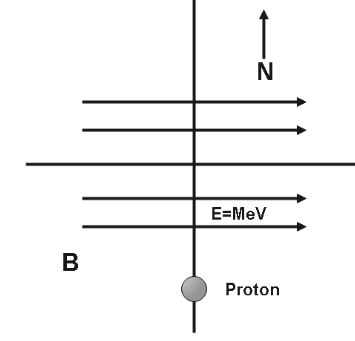
According to the question we have given that,
Kinetic energy of a photon is 1MeV1MeV and we know that 1 eV=1.6×10−19J1\,eV = 1.6 \times {10^{ - 19}}J
1MeV=1×10eV=1.6×10−13J1MeV = 1 \times 10eV = 1.6 \times {10^{ - 13}}J
Therefore, we can say that,
K.E=12mv2=12×1.6×10−27×v2K.E = \dfrac{1}{2}m{v^2} = \dfrac{1}{2} \times 1.6 \times {10^{ - 27}} \times {v^2}
And we have given the mass of the proton i.e., 1.6×10−27kg1.6 \times {10^{ - 27}}kg
Therefore,
1.6×10−13=12×1.6×10−27×v2 ⇒v=2×107m s−1 1.6 \times {10^{ - 13}} = \dfrac{1}{2} \times 1.6 \times {10^{ - 27}} \times {v^2} \\\ \Rightarrow v = \sqrt {2 \times {{10}^7}} m{\text{ }}{s^{ - 1}} \\\
And also, from newton's law we know that, F=maF = ma and in magnet field case the force is equal to BqvBqv
Bqv=maBqv = ma
Now solving for magnetic field,
Bqv=ma ⇒B=maqv ⇒B=1.6×10−27×10121.6×10−19×2×107 Bqv = ma \\\ \Rightarrow B = \dfrac{{ma}}{{qv}} \\\ \Rightarrow B = \dfrac{{1.6 \times {{10}^{ - 27}} \times {{10}^{12}}}}{{1.6 \times {{10}^{ - 19}} \times \sqrt {2 \times {{10}^7}} }} \\\
And now on further solving we get,
B=1.6×10−27×10121.6×10−19×2×107 ⇒B=0.71×10−3 ∴B=0.71 mT B = \dfrac{{1.6 \times {{10}^{ - 27}} \times {{10}^{12}}}}{{1.6 \times {{10}^{ - 19}} \times \sqrt {2 \times {{10}^7}} }} \\\ \Rightarrow B = 0.71 \times {10^{ - 3}} \\\ \therefore B = 0.71\,mT \\\
Hence, option A is the correct answer.

Note: Note that unit conversion is must here because we are solving here in standard units. Otherwise you will get the wrong answer. You must remember the formula of force acting on the magnetic field and the relation between the force and acceleration. Also, for easy understanding, draw the diagram Note that direction of magnetic field is given by cross product.