Question

Period of f\left( x \right)=\sin 3\pi \left\\{ x \right\\}+\tan \pi \left[ x \right] where [ ] and { } represent a GIF and fraction part of x respectively.

& A.1 \\\ & B.2 \\\ & C.3 \\\ & D.\pi \\\ \end{aligned}$$

Answer 1

In this question, we are given a function f\left( x \right)=\sin 3\pi \left\\{ x \right\\}+\tan \pi \left[ x \right]. We need to find its period. For this, we will first prove that $\tan \pi \left[ x \right]$ is zero for any value of x. Then we will use the period of {x} which will give us the period of \sin 3\pi \left\\{ x \right\\}. Hence this period will be our final answer.

Complete step-by-step answer:
Here we are given the function as f\left( x \right)=\sin 3\pi \left\\{ x \right\\}+\tan \pi \left[ x \right].
Let us first examine $\tan \pi \left[ x \right]$. We know that [x] represents the greatest integer function of x. Therefore, the value of [x] will always be an integer.
Now we know that, $\tan n\pi =0$ for any n as an integer. Hence $\tan \pi \left[ x \right]$ will also be 0 because [x] is integer. Therefore, $\tan \pi \left[ x \right]=0$.
Hence our function reduces to f\left( x \right)=\sin 3\pi \left\\{ x \right\\}.
Now we just need to find the period of {x}.
As we know {x} represents the fraction part of x. So, x will always be in fraction form which lies between 0 and 1.
Let us look at the graph of {x}.

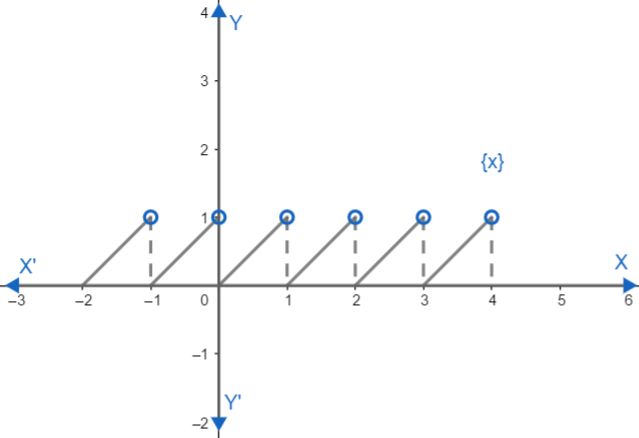
As we can see from the graph that {x} always lies between 0 and 1 and repeats after 1. So the period of {x} is 1.
Now \sin 3\pi \left\\{ x \right\\} depends upon {x} whose period is 1. Therefore, the period of \sin 3\pi \left\\{ x \right\\} will also be 1. Hence option A is the correct answer.

So, the correct answer is “Option A”.

Note: Students should note that {x} (fractional part of x) is different as the difference between x and greatest integer function [x] i.e. {x} = x-[x]. Students should keep in mind that $\sin n\pi =0,\tan n\pi =0$ where n is any integer. Note that, in values of {x} 1 is not included which means 0\le \left\\{ x \right\\}\text{ }<\text{ 1}.