Question
Question: The kinetic energy of four moles of $O_2$ at $27^\circ C$ is (R=8.314$JK^{-1} mol^{-1}$)...
The kinetic energy of four moles of O2 at 27∘C is (R=8.314JK−1mol−1)
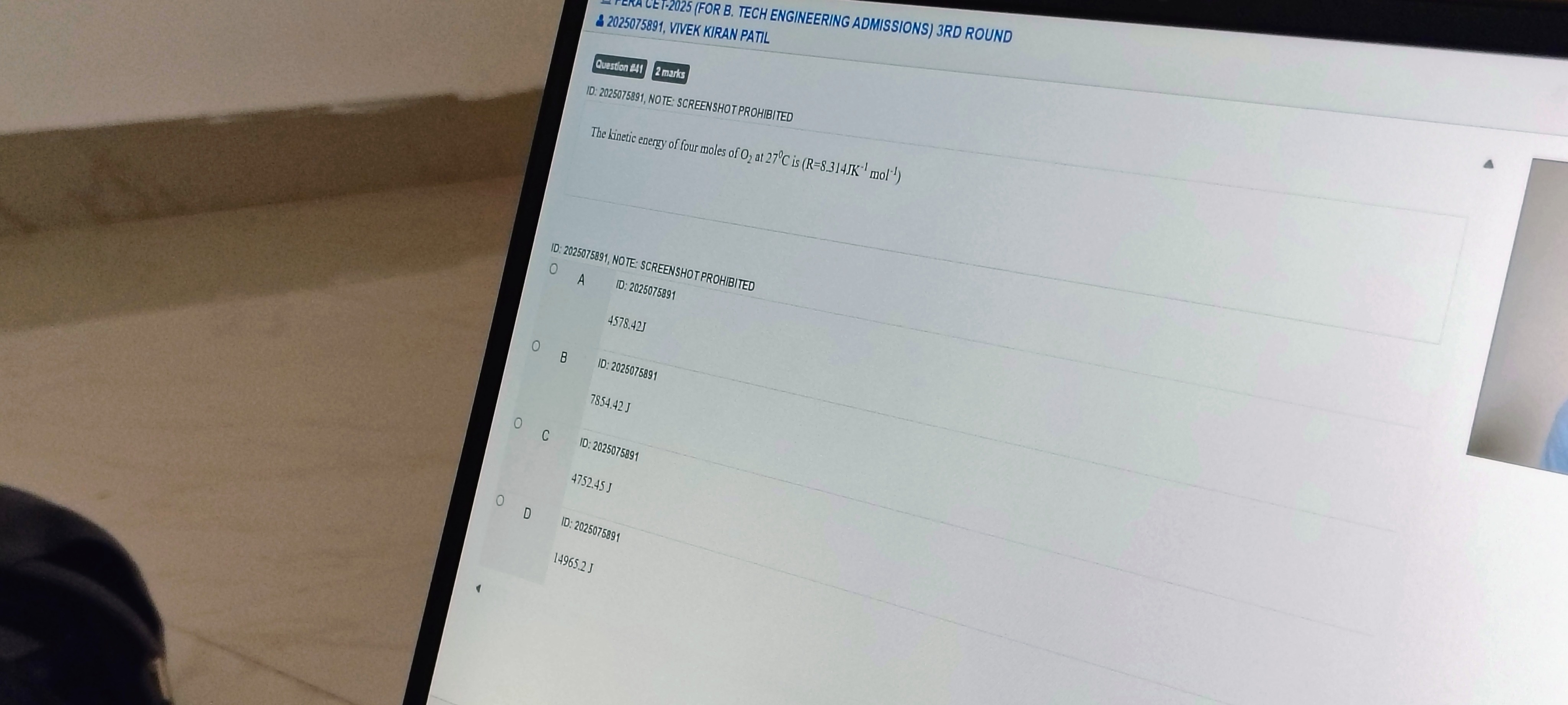
4578.42J
7854.42 J
4752.45 J
14965.2 J
14965.2 J
Solution
The kinetic energy of a gas can refer to its total kinetic energy or specifically its translational kinetic energy.
The formula for the total kinetic energy of n moles of an ideal gas is given by:
E=2fnRT
where:
- f is the degrees of freedom of the gas molecule.
- n is the number of moles.
- R is the universal gas constant.
- T is the absolute temperature in Kelvin.
For oxygen (O2), which is a diatomic gas, the degrees of freedom (f) at moderate temperatures (where vibrational modes are not excited) are 5 (3 translational + 2 rotational).
If we calculate the total kinetic energy using f=5:
Given:
n=4 moles
T=27∘C=27+273=300 K
R=8.314 J K−1 mol−1
f=5 (for total kinetic energy of a diatomic gas)
Etotal=25×4×8.314×300
Etotal=5×2×8.314×300
Etotal=10×8.314×300
Etotal=83.14×300=24942 J
This value (24942 J) is not among the given options.
However, sometimes "kinetic energy" in such problems implicitly refers to the translational kinetic energy, which is common for all gases and is directly related to temperature. The formula for translational kinetic energy is derived from the average translational kinetic energy per molecule, 23kT, and scales up to n moles as 23nRT.
In this case, the degrees of freedom considered are only the translational ones, so f=3.
Let's calculate the translational kinetic energy using f=3:
Etranslational=23nRT
Etranslational=23×4×8.314×300
Etranslational=3×2×8.314×300
Etranslational=6×8.314×300
Etranslational=49.884×300
Etranslational=14965.2 J
This value (14965.2 J) matches option D. Given that one of the options matches exactly with this interpretation, it is highly probable that the question intends to ask for the translational kinetic energy.
